1 .1 Анализ глобальной навигационной спутниковой системы и построение структуры системы безопасности на основе позиционирования

Глобальные Навигационные Спутниковые Системы (ГНСС) представляют собой всепогодные системы космического базирования, позволяющие в глобальных масштабах определять текущие местоположения подвижных объектов и их скорость, а как же осуществлять точную координацию системного времени.

Спутниковую радионавигационную систему можно рассматривать как высокотехнологичную информационную систему, состоящую из пяти основных сегментов. Основные сегменты и связи между ними указаны на рисунке 1 [1].

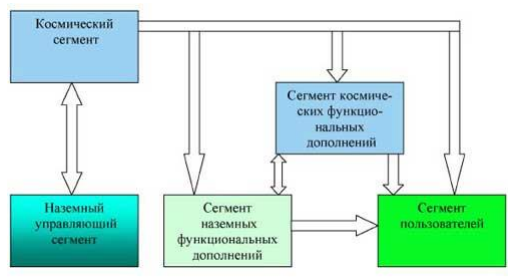
Рисунок 1.1 – Организация спутниковой радионавигационной системы

Наземный управляющий сегмент включает в себя центр управления космическим сегментом, станции слежения за навигационными спутниками (радиолокационные и оптические), аппаратуру контроля состояния навигационных спутников. Управляющий сегмент решает задачи определения, прогнозирования и уточнения параметров движения навигационных спутников, формирования и передачи в бортовую аппаратуру спутников цифровой информации, а также ряд контрольных и профилактических функций.

Космический сегмент представляет собой систему навигационных спутников, вращающихся по эллиптическим орбитам вокруг Земли. На каждой орбите находятся несколько навигационных космических аппаратов, имеющих на борту радиоэлектронную аппаратуру, излучающую в направлении Земли шумоподобные непрерывные радиосигналы, содержащие информацию необходимую для проведения навигационных определений с помощью аппаратуры потребителя.

Сегменты наземных и космических функциональных дополнений представляет собой аппаратурно-программные комплексы предназначенные для обеспечения точности навигационных определений, целостности, непрерывности, доступности и эксплуатационной готовности системы [2].

Сегмент пользователей потенциально может состоять из неограниченного количества спутниковых навигационных приемников, которые принимают сигналы навигационных спутников и производят расчеты текущего местоположения, скорости и времени с погрешностями, определяемыми спутниковой навигационной системой и аппаратурой потребителя.

Глобальная система позиционирования (GPS, ГЛОНАСС – обеспечивающие измерение времени и расстояния навигационных спутников) – спутниковая система навигации, позволяющая в любом месте Земли (не включая приполярные области), почти при любой погоде, а также в космическом пространстве вблизи планеты определить местоположение и скорость объектов.

Основной принцип использования системы – определение местоположения путем измерения расстояний до объекта от точек с известными координатами – спутников. Расстояние вычисляется по времени задержки распространения сигнала от посылки его спутником до приема антенной GPS-приемника. То есть, для определения трехмерных координат GPS-приемнику нужно знать расстояние до трех спутников и время GPS системы. Таким образом, для определения координат и высоты приемника, используются сигналы как минимум с четырех спутников.

Основой системы являются навигационные спутники, движущиеся вокруг Земли по 6 круговым орбитальным траекториям (по 4 спутника в каждой), высотой примерно 20180 км. Спутники излучают открытые для использования сигналы в диапазонах: 1575,42 МГц, 1227,60 МГц и 1176,45 МГц. Навигационная информация может быть принята антенной (обычно в условиях прямой видимости спутников) и обработана при помощи GPS-приемника.

24 спутника обеспечивают 100 % работоспособность системы в любой точке земного шара, но не всегда могут обеспечить уверенный прием и хороший расчет позиции. Поэтому, для увеличения точности позиционирования и резерва на случай сбоев, общее число спутников на орбите поддерживается в большем количестве.

Типичная точность современных GPS-приемников в горизонтальной плоскости составляет примерно 6–8 метров при хорошей видимости спутников и использовании алгоритмов коррекции. На территории США и Канады имеются станции WAAS (система распространения поправок к данным), передающие поправки для дифференциального режима, что позволяет снизить погрешность до 1–2 метров на территории этих стран. При использовании более сложных дифференциальных режимов, точность определения координат можно довести до 10 см. К сожалению, точность любой спутниковой навигационной системы сильно зависит от открытости пространства, от высоты используемых спутников над горизонтом.

Общим недостатком использования любой радионавигационной системы является то, что при определенных условиях сигнал может не доходить до приемника, или приходить со значительными искажениями или задержками. Например, практически невозможно определить свое точное местонахождение в глубине квартиры внутри железобетонного здания, в подвале или в тоннеле. Так как рабочая частота GPS лежит в дециметровом диапазоне радиоволн, уровень приема сигнала от спутников может серьезно ухудшиться под плотной листвой деревьев или из-за очень большой облачности. Нормальному приему сигналов GPS могут повредить помехи от многих наземных радиоисточников, а также от магнитных бурь.

Структура системы безопасности на основе позиционирования представлена на рисунке 1.2 [3].

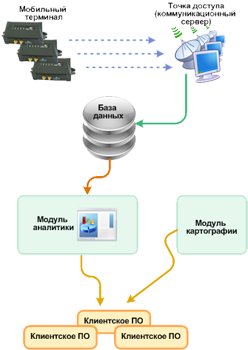
Рисунок 1.2 – Структура системы безопасности на основе позиционирования

Система безопасности, основанная на получение и обработки сигналов с различных спутниковых систем и передача актуальной информации в любой момент времени – это программно-аппаратный комплекс, использующий для определения координат контролируемого подвижного объекта, систему спутниковой навигации GPS и технологию GPRS в сетях сотовой связи (GSM) для передачи отчетов на сервер.

Система GPS мониторинга состоит из трех основных компонентов: аппаратная навигационная часть, серверная часть, клиентская часть. Спутниковая система GPS мониторинга обеспечивает такую важную составляющую процесса управления, как контроль и позволяет узнать точное местоположение объекта.

Мобильный GPS терминал является аппаратной навигационной частью и предназначен для определения координат и параметров работы контролируемого объекта (обычно транспортного средства), промежуточного хранения и передачи данных в точку доступа.

Точка доступа принимает данные от GPS терминала, преобразует их в форму, удобную для хранения в базе данных и складывает их в базу данных. В системе мониторинга транспорта может существовать несколько точек доступа – основная и резервная, а также специализированных на обработке того или иного типа мобильных терминалов.

База данных обеспечивает хранение и выдачу данных. В масштабных системах мониторинга может быть несколько баз данных, каждая из которых «специализирована» для хранения данных о группе терминалов или приближена в Web-пространстве к месту эксплуатации остальных элементов системы.

Модуль аналитики готовит аналитические отчеты за выбранный период времени по запросу клиентского ПО – рассчитывает величину параметров и счетчиков, считывает информацию с датчиков, установленных и подключенных к GPS терминалу

Модуль картографии хранит и выдает по запросу клиентского ПО изображение карт.

Клиентская часть представляет собой программу, работающую на обычном компьютере, имеющим любой доступ к Интернету. При работе получает информацию как в реальном времени, так и историю с серверной базы данных, в которой хранятся данные GPS слежения о контролируемых объектах. Такое построение системы GPS мониторинга позволяет диспетчеру подключаться к Интернету периодически, в отличии от серверного оборудования. Данные из базы данных отображаются на электронной карте местности, где находится объект. Система GPS мониторинга допускает любое количество подключений, разнесенных территориально и контролирующих одни и те же объекты. Например, за автопарком постоянно наблюдает диспетчер и при этом руководитель может в любой момент из любого места проконтролировать интересующий его автомобиль, за любой период имея ноутбук и возможность подключения к сети Internet.

В конкретных реализациях систем GPS мониторинга отдельные элементы представленной схемы могут быть совмещены друг с другом: часто совмещается клиентскую часть и модуль аналитики.

Подобная система безопасности применима как для контроля объектов различного назначения (товары, транспорт и т.д.), так и для контроля для определения местонахождения людей, животных.

Анализируя общую информацию о работе и построение системы безопасности на основе позиционирование можно прийти к выводу, что использование спутниковой радионавигационной системы в целях безопасности и навигации особенно эффективно. Главной задачей в данном случае является повышение достоверности навигационных определений. Эта проблема решается двумя путями:

• обеспечение целостности спутниковой радионавигационной системы, отсутствие неисправной космической составляющей системы;

• повышение помехоустойчивости приемников, в том числе в условиях воздействия преднамеренных помех. Этот путь включает: улучшение алгоритмов обработки сигналов, обеспечивающих снижение порогового отношения сигнал/шум, пространственно-временную обработку сигналов и комплексирование с другими системами.

В настоящее время способом для существенного повышения точности навигационных определений связаны с созданием глобальной системы отсчета, путем итерации двух спутниковых навигационных систем – ГЛОНАСС и GPS. Исходя из этого можно выделить четыре основных направлений модернизации спутниковой радионавигационной системы ГЛОНАСС:

• улучшение совместимости с другими радиотехническими системами;

• повышение точности радионавигационных определений и улучшение сервиса, предоставляемого пользователям;

• повышение надежности и срока службы бортовой аппаратуры спутников и улучшение целостности системы;

• развитие дифференциальной подсистемы [3].

Анализ глобальной навигационной спутниковой системы показал, что существуют много различных путей повышения эффективности работы системы и удобство ее эксплуатации.

1.2 Методы и принципы определения координат

1 .2 Методы и принципы определения координат и поиска сигналов в глобальной навигационной спутниковой системе

Орбитальная группировка системы GPS содержит 24 штатных навигационных космических аппаратов (спутников) на круговых синхронных орбитах с периодом обращения Т = 12 ч 00 мин (высота орбиты составляет около 20 000 км над поверхностью Земли) в шести орбитальных плоскостях (по четыре аппарата в каждой) с наклонением 55°, долготы восходящих узлов которых смещены с интервалом 60°.

Система GPS работает следующим образом. В каждый момент времени GPS-приемнику известно точное местонахождение навигационных космических аппаратов. Координаты могут быть вычислены для места на поверхности Земли по измерениям расстояний от группы космических аппаратов (если их положение в космосе известно). В этом случае навигационные космические аппараты являются пунктами с известными координатами. Если расстояние от одного навигационного космического аппарата известно, то можно описать сферу заданного радиуса вокруг него. Сфера заданного радиуса космического аппарата показана на рисунке 1.3 [3].

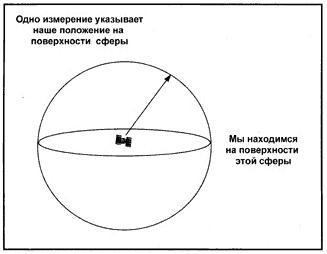
Рисунок 1.3 – Сфера заданного радиуса космического аппарата

В случае если известно расстояние и до второго навигационного космического аппарата, то определяемое местоположение будет расположено в круге, задаваемом пересечением двух сфер. Пересечение двух сфер показано на рисунке 1.4 [3].

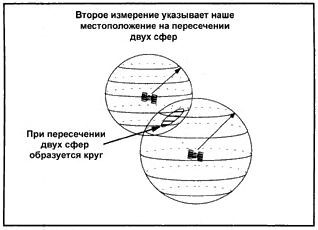
Рисунок 1.4 – Пересечение двух сфер

Третий навигационный космический аппарат определяет две точки на окружности, при этом остается выбрать правильную точку.

Одна из точек всегда может быть отброшена, т.к. имеет высокую скорость перемещения или находится на, или под поверхностью Земли. Таким образом, зная расстояние до трех навигационных космических аппаратов, можно вычислить координаты определяемой точки (GPS-приемники могут быстро вычислить истинную точку из двух).

Приняв сигнал не менее чем от трех навигационных космических аппаратов можно вычислить координаты любой точки около поверхности Земли. Но для точных вычислений координат необходимо использовать высокоточные часы. Это необходимо потому, что ошибка во времени всего в 0.001 с дает ошибку определения местоположения в 300 км. Именно поэтому на каждом из навигационных космических аппаратов GPS установлены атомные часы, причем не одни, а в четырех экземплярах, чтобы гарантировать, что, хотя бы одни из них будут работать в любом случае. Атомные часы на спутнике дают точность 10-9 с.

Расстояние до навигационного космического аппарата определяется по измерениям времени прохождения радиосигнала от аппарата до GPS-приемника умноженным на скорость света. Для того, чтобы определить время распространения сигнала необходимо знать, когда он покинул навигационный космический аппарат. Для этого на спутнике и в приемнике одновременно генерируется одинаковый псевдослучайный код.

GPS-приемник проверяет входящий сигнал с космического аппарата и определяет, когда он генерировал такой же код. Полученная разница, умноженная на скорость света (~3×105 км/с) дает искомое расстояние.

Использование кода позволяет GPS-приемнику определить временную задержку в любое время. Навигационные системы GPS излучают сигнал на одной и той же частоте, т.к. каждый навигационный космический аппарат идентифицируется по своему псевдослучайному коду (PRN или Pseudo Random Number code).

Вычисления напрямую зависят от точности хода часов. Код должен генерироваться на спутнике и GPS–приемнике в одно и то же время. На навигационном космическом аппарате установлены атомные часы, имеющие точность около одной наносекунды. Однако это слишком дорого, чтобы устанавливать такие часы в каждый GPS-приемник, поэтому измерения от четвертого космического аппарата используются для устранения ошибок хода часов приемника [5].

Альманах и эфимерис.

Все навигационные космические аппараты передают два вида данных – альманах и эфимерис. Альманах содержит параметры орбит всех спутников. Каждый спутник передает альманах для всех других навигационных космических аппаратов. Данные альманаха не отличаются большой точностью и действительны несколько месяцев.

В свою очередь, данные эфимериса содержат очень точные корректировки параметров орбит и часов для каждого спутника, что требуется для точного определения координат. Каждый GPS спутник передает только данные своего собственного эфимериса. Эти данные действительны только 30 минут. Спутники передают свой эфимерис каждые 30 секунд.

Если GPS был отключен более 30 минут, а потом включен, он начинает искать спутники, основываясь на известном ему альманахе. По нему GPS выбирает спутники для инициации поиска.

Если питание приемника отключить, а потом снова включить в течение 30 минут, он определит спутники очень быстро, т.к. не надо будет снова собирать данные эфимериса. Это называется «горячий» старт.

Если после отключения прошло более 30 минут, будет произведен «теплый» старт и GPS приемник снова начнет собирать данные эфимериса.

Если GPS приемник был перевезен (в выключенном состоянии) на несколько сотен километров или внутренние часы стали показывать неточное время, то данные имеющегося альманаха являются неверными. В таком случае приемнику требуется выполнить новый поиск (переинициализацию) для загрузки нового альманаха и эфимериса. Это уже будет «холодный» старт [4].

Виды сигналов навигационных космических аппаратов.

Схема формирования сигналов спутника системы GPS содержит два несущих колебания частотой 1575.42 МГц (L1) и 1227.6 МГц (L2), которые модулируются в фазовых модуляторах 3–4 (манипуляции фазы несущего колебания на 180°) псевдослучайными сигналами С/А– и Р-кода, предварительно просуммированными по модулю 2 элементами 1, 2 исключающее или с навигационным сигналом NAV, который передается со скоростью 50 бит/с. На рисунке 1.5 [5] показано, что несущая L2 модулируется только суммарным сигналом Р–кода, тогда как L1 – суммарными сигналами С/А– и Р–кода.

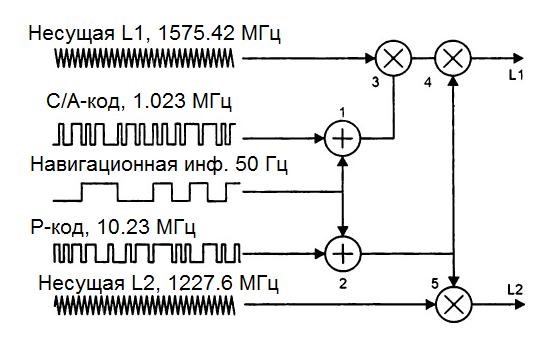
Рисунок 1.5 – Сфера заданного радиуса космического аппарата

В результате фазовой модуляции (манипуляции) ширина полосы сигнала, несущего информацию, увеличивается со 100 Гц (удвоенная частота навигационных посылок 50 Гц) до 20,46 МГц (для кода Р) и до 2,046 МГц (для кода С/А).

Р-код предназначен для высокоточных измерений (в режиме PPS – Precise Positioning Service) после заведения в 1994 году дополнительной криптозащиты (A/S – Anti-Spoofing) он обозначается как P(Y)). Поскольку этим кодом модулируются обе несущие, то сравнение времени прихода сигналов на частотах L1 и L2 позволяет вычислять дополнительную задержку, возникающую при прохождении сигналов через ионосферу, что значительно повышает точность измерений. Заметим, что некоторые приемники компании Trimble геодезического класса работают с Р-кодом.

Общедоступный код С/А (Coarse Acqusition — грубый захват) используется в режиме SPS (Standart Positioning Service — стандартная точность измерений).

Если в режиме PPS ошибка измерения горизонтальных координат не превышают 22 м, высоты — 27.7 м и времени — 0.09 мкс, то в SPS-режиме она увеличивается соответственно до 100 м, 140 м и 0.34 мкс [5].

Основные методы поиска сигналов глобальной навигационной спутниковой системы.

Принимаемые приемником сигналы глобальной навигационной спутниковой системы GPS можно охарактеризовать следующими параметрами: наложенная на сигнал псевдослучайная последовательность, индивидуальная для каждого НКА; доплеровское смещение частоты и время задержки – время от момента излучения сигнала до момента его приема.

Точное определение момента приема требует знания доплеровской отстройки по частоте и сдвига принимаемой псевдослучайной последовательности относительно генерируемой в навигационном пользовательском устройстве.

Таким образом, т.к. эти параметры являются неизвестными, при обнаружении требуется осуществить перебор по всем возможным значениям обоих параметров.

Время обнаружения стремятся сократить к минимуму, перебор по одному из параметров можно осуществлять параллельно.

При этом выделяют две основных схемы. Первая схема, приведенная на рисунке 1.6 [5], является последовательной по частоте и последовательно-параллельной по задержке или сдвигу кода.

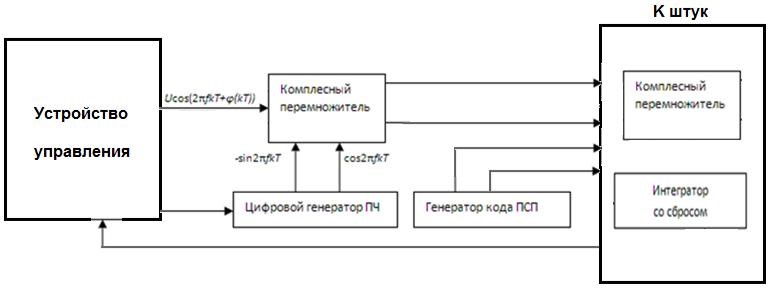
Рисунок 1.6 – Последовательная по частоте схема поиска сигналов спутников системы GPS

Устройство управления отвечает за управление остальными элементами схемы. Входной сигнал представляет собой перенесенный на промежуточную частоту оцифрованный сигнал с входной антенны.

Выражения, описывающие последовательную по частоте задержку или сдвиг кода представлены в выражении 1.1:

где индекс ∆fm соответствует m-му шагу по доплеровскому смещению.

Добавка к фазе отражает влияние эффекта Доплера [11]. Последовательно меняя частоту генератора с нужным шагом, обеспечиваем перебор требуемого диапазона доплеровского смещения. Параллельность при поиске смещения псевдослучайной последовательности достигается за счет использования К штук модулей, включающих комплексный умножитель и интегратор. Генератор кода псевдослучайной последовательности включает в себя линию задержки на элементов.

Второй вариант заключается в использовании преобразования Фурье для параллельного поиска по частоте. На вход дискретного преобразования фурье (ДПФ) поступает результат комплексного умножения входной и опорной последовательностей. Размерность ДПФ будет соответствовать числу перебираемых доплеровских сдвигов, после ДПФ требуется такое же число сумматоров.

Параллельная по частоте схема поиска сигналов навигационных космических аппаратов приведена на рисунке 1.7 [5].

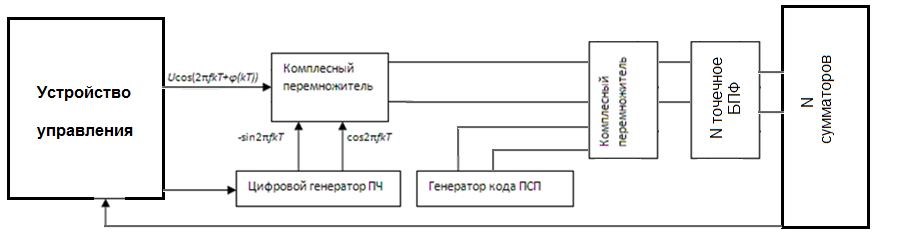
Рисунок 1.7 – Параллельная по частоте схема поиска сигналов спутников

системы GPS

Выражения, описывающие параллельную по частоте задержку или сдвиг кода представлены в выражении 1.2 [5]:

где индекс k соответствует сдвигу псевдослучайной последовательности.

На выходе каждого сумматора получаем результат для соответствующего доплеровского сдвига и заданного на входе смещения псевдослучайной последовательности.

Существует ряд экзотических схем, сочетающих в себе преимущества, как первого, так и второго подхода, однако они эффективно работают только при определенных условиях, поэтому рассмотрены не будут.

Дифференциальный режим DGPS.

Учитывая точность, приемлемую для потребителя, и характеристики использующегося приемного устройства GPS, можно выделить несколько методов для получения координат при помощи GPS. Данными методами являются: автономная навигация, дифференциальные фазовые измерения, дифференциальное координирование.

При автономной навигации применяется только один (автономный) приемник. Данный метод используется туристами, штурманами для навигации судов, находящихся вдали от берега и военными. Точность определения координат около 100 м для гражданских потребителей и приблизительно 20 м для военных потребителей.

Дифференциальные фазовые измерения помогают достичь точности 0,5–20 мм. Этот метод получения координат применяется для геодезических измерений, управления строительной техникой и т.д. При использовании дифференциального координирования DGPS, погрешность спутниковых измерений составляет 0,5–5 м. DGPS – весьма простая для использования GPS приемником методика, при которой координаты места и/или точного времени могут быть получены мгновенно. Получаемая точность может быть выше 100 м (ранее – 30–50 м) для гражданских пользователей и 5–15 м для военных [4].

Дифференциальная навигация основана на относительном постоянстве значительной части погрешностей навигации во времени и в пространстве. При использовании дифференциального режима спутниковой системе необходимо два навигационных приемника (контрольно-корректирующая станция и потребитель), располагающихся в двух точках пространства. При этом дифференциальная контрольно-корректирующая станция (базовая станция) геодезически точно подвязана к принятой системе координат. Разности между измеренными и рассчитанными в ней значениями псевдодальностей спутников в области видимости, а также разности между измеренными и рассчитанными псевдоскоростями по линии передачи данных передаются потребителю. Эти разности называют дифференциальными поправками [5]. Потребитель же вычитает полученные поправки из измеренных псевдодальностей и псевдоскоростей. В случае, когда неточности определения псевдодальностей почти не меняются во времени и пространстве, погрешности значительно компенсируются поправками, переданными по линии передачи данных. Основными слабо меняющимися погрешностями определения псевдодальности являются ошибки синхронизации, погрешности за счет ошибок эфемеридного обеспечения, некомпенсированные ионосферные погрешности. С использованием дифференциальной DGPS неточности определения места снижаются до метров и ниже. Дифференциальный режим осуществляется с помощью контрольного- корректирующего навигационного приемного устройства, называемого базовой станцией. Базовую станцию устанавливают в точке с известными геодезическими координатами. При сравнении имеющихся координат (полученных в результате прецизионной геодезической съемки) с измеренными координатами базовым навигационным приемником формируются поправки, передающиеся потребителям по каналам связи. Приемник потребителя учитывает принятые от базовой станции поправки при решении навигационной задачи. Это дает возможность определить его координаты с точностью до одного метра. Результаты, полученные при помощи дифференциального метода, в большей степени зависят от расстояния между потребителем и базовой станцией. Использование данного метода наиболее результативно, когда преобладающими являются систематические ошибки, вызванные внешними (по отношению к приемнику) факторами. Данные ошибки в значительной мере компенсируются при близком расположении базовой станции к приемному устройству потребителя. Поэтому зона обслуживания базовой станции не превышает 500 км. Дифференциальные поправки могут передаваться от базовой станции к потребителю с помощью телефонной или радиосвязи, по системам спутниковой связи (например, INMARSAT), а также с применением технологии передачи цифровых данных RDS (Radio Data System) на рабочих частотах FM-радиостанций. На сегодняшний день в некоторых странах уже функционирует развитая сеть базовых (дифференциальных) станций, постоянно передающих поправки на определенную территорию [5].

Современные дифференциальные системы спутниковой навигации состоят из систем дифференциальной навигации по кодовым и псевдофазовым измерениям. Системы дифференциальной навигации по кодовым измерениям основаны на измерении и обработки псевдодальностей, в общем, обладают неограниченной областью действия и определяются неточностями определения места от долей до нескольких метров. Системы дифференциальной навигации по псевдофазовым измерениям характеризованы весьма высокой точностью позиционирования (до долей сантиметра). Но все же область их действия ограничивается дальностью 10-12 км в одночастотном режиме и 100 км в двухчастотном режиме. Специфической особенностью дифференциальных систем по псевдофазовым измерениям можно назвать неоднозначность данных измерений, которая затрудняет их использование. Системы дифференциальной навигации по псевдофазовым измерениям иногда называют системами относительных определений [6].

Системы дифференциальной навигации по кодовым измерениям могут быть локальными, широкодиапазонными и глобальными. Множество современных систем дифференциальной навигации являются локальными. Локальные дифференциальные системы применяют единственную наземную станцию измерений и формирования дифференциальных поправок (дифстанций). Дифстанция обычно размещается в центральной части локальной зоны, габариты которой составляют не более 200 км. В центре зоны достигается точность измерений приблизительно 0,5–1 м. На граничной части зоны точность снижается и постепенно приближается к точности абсолютных местоопределений. Дифференциальные поправки в локальных системах дифференциальной навигации могут быть сформированы на основании метода коррекции координат и метода коррекции навигационных параметров. Большее практическое распространение получил второй метод, в котором дифстанция создает поправки к измерениям псевдодальностей для каждого из видимых ею спутников. Пользователь поправляет свои измерения псевдодальностей по тем же спутникам на значения, полученные от дифстанции. Для передачи поправок, сформированных в соответствии с методом коррекции навигационного параметра, был разработан специальный стандарт RTCM SC– 104, который учитывает особенности современной системы позиционирования GPS [8].

В широкодиапазонных системах дифференциальной навигации (WADGPS) применяется сеть станций сбора информации (ССИ) и совершенно отличный от других метод получения дифференциальных поправок. Этот метод был назван the state-space approach (метод коррекции параметров моделей движения КА, свойств модели ионосферных задержек и смещений шкал времени навигационных спутников). В широкодиапазонных системах измерения двухчастотных навигационных приемников, размещенных на станциях сбора информации (ССИ), собираются в единый центр, где проходит их совместная обработка для оперативного уточнения параметров моделей движения космических аппаратов, смещения шкал времени спутников и формирования карт вертикальных ионосферных задержек. Все перечисленные данные далее оперативно передаются тем или иным способом потребителю, который применяет их для уточнения данных, извлекаемых им из сигналов навигационных спутников. Широкодиапазонные системы дифференциальной навигации помогают получить точность определения места со среднеквадратической ошибкой 0,5 м в области, охватываемой сетью ССИ, и соседних с ней областях. Между ошибками оценки смещений шкал времени и ошибками оценки вертикальных координат приемника осуществляют сильную корреляцию. Такая корреляция может возникнуть из-за абсолютной схожести соответствующих частных производных, особенно для спутников с большими углами возвышения. Стабилизация опорных частот приемников ССИ и приемника пользователя при помощи рубидиевых генераторов помогает лучше разделять ошибки оценки смещения шкал времени и вертикальных координат приемника. Результаты соответствующих экспериментов демонстрируют среднеквадратические ошибки вертикальных координат меньше 0,4 м [10].

Неосновным, но весьма значимым параметром широкодиапазонных системы дифференциальной навигации. Первая система WADGPS принадлежит фирме Satloc. Вторая система WAAS (Wide Area Augmentation System) находится в управлении правительства США. В системе WADGPS пользователю выдается карта вертикальных ионосферных задержек с шагом 2°. В системе WAAS, зависимо от класса точности, потребитель имеет возможность применять карты вертикальных ионосферных задержек разнличной точности. Наиболее подробные карты содержат до 929 точек прокола ионосферы [11].

Параметры системы WADGPS фирмы Satloc по сравнению с параметрами системы WAAS имеют некоторые различия. Задержка формирования корректирующих поправок в системе фирмы Satloc составляет 4 с, а системе WAAS – 6 с. Satloc использует только 15 ССИ. WAAS использует избыточное число из 24–х ССИ, расположенных как на континентальной территории США, так и на Аляске и Гавайских островах. Для того, чтобы удовлетворить строгим требованиям доступности, обеспечивающих высокую степень целостности, система WAAS требует два или более геостационарных спутника, излучающих дополнительные дальномерные коды. Скорость передачи корректирующей информации в системе фирмы Satloc равна 750 бит/с, а в системе WAAS приблизительно 250 бит/с. Корректирующая информация в системе фирмы Satloc квантуется с дискретом 1/16 м, а в системе WAAS – с дискретом 1/8 м [10].

Работа широкодиапазонных систем дифференциальной навигации базируется на применении трех основных категорий программного обеспечения. К первой категории относится программное обеспечение уточнения параметров орбит и смещения временных шкал спутников. Второй тип программного обеспечения - составление содержательных карт вертикальных ионосферных задержек. К третьему виду относится программное обеспечение, обеспечивающее постоянную работу наземной сети дифференциальной системы в режиме реального времени. Выделяют статический, кинематический и динамический методы уточнения параметров орбит и смещения временных шкал спутников. В статическом методе содержится решение так называемой вывернутой навигационной задачи. С помощью обработки измерений двухчастотных навигационных приемников, проводимых в одно и то же время из нескольких наземных точек с известными координатами, мгновенно определяется местонахождение и смещение временных шкал спутников, расположенных в области видимости наземных станций. В этом случае не берется в учет динамическая информация, заключающаяся в жесткой коррелированности пространственного положения спутников в смежные моменты времени. В кинематическом методе дополнительно оцениваются составляющие мгновенного вектора скорости также без учета динамической информации. В наиболее точном и совершенном динамическом методе проводится оценка определенного набора параметров орбиты, смещения временных шкал спутников и наземных станций, а также некоторых дополнительных параметров, порождающих модельные значения измерений наилучшим образом, согласующиеся с результатами реальных измерений на длительных интервалах времени. Значимым преимуществом динамического метода можно назвать его способность эффективно делить оценки эфемерид и смещения временных шкал, что повышает целостность системы. В случае, когда информация о движении спутника останется незамеченной, проводить раздельную оценку эфемерид и смещения временных шкал будет затруднительно, и точная оценка возможна только для суммы обоих компонентов.

В программном обеспечении уточнения параметров орбит и смещения шкал времени спутников в системе WAAS и дифференциальной системе фирмы Satloc используются алгоритмы из хорошо протестированного и обеспечивающего высокой точностью пакета прикладных программ GIPSY/OASIS II (GOA II). Данный пакет применяет динамический метод, обладает богатой историей развития и широко используется для высокоточного определения орбит различных космических аппаратов (в том числе, спутников GPS), а также в целях высокоточной спутниковой геодезии. Разработчиком и владельцем пакета GOA II является Лаборатория реактивного движения Калифорнийского технического института. Исходный пакет GOA II состоит по большей части из фортранных программ и UNIX–сценариев, что сильно затрудняет его использование в масштабе реального времени и среде, отличной от UNIX. Для преодоления этих ограничений JPL на основе пакета GOA II разработало новый пакет Real-Time Gipsy (RTG). Этот пакет предназначен для использования в системах широкодиапазонной дифференциальной навигации и прочих системах реального времени, например, в проектах NASA по определению орбит на борту космических аппаратов и определению координат радиолокатора с синтезированной апертурой на самолете в реальном масштабе времени. WAAS и дифференциальная система фирмы Satloc используют для уточнения параметров орбит и смещения шкал времени спутников пакет RTG, лицензированный JPL [11].

В пакете прикладных программ GIPSY/OASIS II (GOA II) оцениваются координаты и составляющие вектора скорости спутников на некоторый узловой момент, смещение шкал времени спутников и наземных пунктов, тропосферные искажения и коэффициент солнечного давления. Указанные параметры оцениваются по измерениям на 30-часовых интервалах [11].

В результате точность определения траектории возрастает более чем в три раза, по сравнению с точностью орбит, параметры которых передаются в навигационных сообщениях спутников. Среднеквадратические ошибки по радиусу, поперек и вдоль орбиты для указанного выше случая составляют соответственно 0,65, 1,37 и 1,96 м.

Обработка измерений осуществляется путем фильтрации относительно опорной траектории. Для фильтрации используется Square Root Information Filter (SRIF), обладающий повышенной численной устойчивостью, по сравнению с non-square root implementations. В предположении отсутствия проблем вычислительной устойчивости SRIF эквивалентен Калмановскому фильтру.

В основе метода, называемого nonlinear static estimation (NSE), лежит вычисление оценок параметров простой модели вертикальных ионосферных задержек Клобучара, обеспечивающих наилучшее согласование модельных данных с результатами измерений. Измерения извлекаются из двухчастотных измерений навигационных приемников, установленных на станциях сбора информации. Второй метод использует модифицированную версию пакета программ Global Ionosphere Map (GIM), разработанного JPL. Пакет программ GIM содержит программы на Фортране и UNIX–сценарии. Для увеличения мобильности и удобства работы в реальном масштабе времени JPL разработала на основе GIM новый пакет программ - Real Time Ionosphere (RTI), предлагаемый ею для лицензионного использования. В GIM и RTI ионосфера представляется как оболочка над Землей в системе координат, фиксированной относительно Солнца. Ионосфера в такой системе не зависит от вращения Земли и, следовательно, не зависит от местного времени. Оболочка дискретизуется на треугольные элементы. Значение интегральной электронной концентрации (ТЕС) в вершине каждого треугольника трактуется как случайный параметр и оценивается с помощью Калмановского фильтра. Начальные ограничения задаются моделью Бента. Широкодиапазонная система дифференциальной навигации фирмы Satloc для вычисления карт вертикальных ионосферных задержек использует пакет RTI, лицензированный JPL. По своей структуре глобальные системы дифференциальной навигации очень схожи с широкодиапазонными системами. Они тоже применяют наземную сеть станций сбора информации и тот же метод создания дифференциальных поправок. Главное различие состоит в том, что исключение ионосферных ошибок в глобальных системах дифференциальной навигации происходит при использовании двухчастотных измерений. Перспективы введения гражданских кодов в диапазоне L2 в GPS сделают двухчастотные измерения общедоступными. Исключение необходимости вычислять подробные карты вертикальных ионосферных задержек позволяет сильно снизить плотность станций наземной сети. Для этих целей достаточно иметь 12 хорошо расположенных по всему миру станций сбора информации. Для реальных экспериментов использовалось 18 из порядка 60 станций всемирной глобальной сети GPS (Global GPS Network, GGN) принадлежащей NASA, которые оборудованы двухчастотными навигационными приемниками. Необходимо ввести избыточных станций и довести их количества до 25–30. Введение избыточных станций позволяет увеличить точность и надежность дифференциальной системы. В настоящее время можно указать на существование пока что единственной в мире глобальной системы дифференциальной навигации, использующей в качестве основы станции глобальной GPS сети (GGN) NASA. Для оперативного уточнения орбит навигационных спутников в этой системе используется тот же пакет прикладных программ RTG (Real Time Gipsy), который используется для уточнения орбит в широкодиапазонных дифференциальных системах фирмы Satloc и WAAS [12].

1 .3 Методы реализации навигационных устройств на программируемой элементной базе для подвижных объектов

Современная элементная база позволила перейти от последовательной обработки сигналов различных навигационных космических аппаратов к более быстрым методам – параллельному и квазипараллельному. Квазипараллельный метод основан на быстром переключении между сигналами от разных навигационных космических аппаратов, за счет высокой (порядка 2 мс для 2–4 каналов, растет с ростом числа каналов) скорости переключения.

Приемники, которые отслеживают 4 или более навигационных космических аппаратов одновременно (параллельная обработка), могут выдавать мгновенные положение и скорость. Это очень ценно для применения на высокодинамичных объектах и при высокоточных измерениях. Эти устройства часто используются в геодезии и для научных целей. Они могут иметь от 4–х до 10...12 и даже до 24–х каналов слежения [20].

Кроме очевидного преимущества – непрерывного измерения координат местоположения и скорости, эти многоканальные приемники могут также упростить проблему с GDOP (геометрическое снижение точности в случае, когда спутники в области видимости находятся слишком близко друг к другу). Вместо того чтобы строить вычисления на основе сигналов четырех наилучшим образом расположенных спутников, некоторые из этих систем обрабатывают совместно сигналы всех видимых в настоящий момент спутников. Применение к этой избыточной информации соответствующих алгоритмов обработки позволяет получить абсолютный минимум коэффициента увеличения ошибок местоопределения GDOP [21].

Однако стоит учитывать, что рост числа обрабатываемых сигналов навигационных космических аппаратов приводит к росту требуемых для реализации ресурсов пользовательских устройств. Таким образом, важным этапом создания пользовательской составляющей на принципах параллельной обработки является обоснованный выбор этого числа.

GPS-приемники, позволяющие осуществлять параллельный прием, как правило, выполняют в виде систем на одном кристалле (SoC) [21]. В состав такой системы входит специализированная интегральная микросхема ASIC и опционально микроконтроллер или микропроцессор. Возможен так же вариант, когда требуется подключение к персональному компьютеру, где будут выполняться все требуемые для определения положения операции.

Альтернативой для ASIC является применение FPGA. Наличие разных технологий, таких как ASIC и FPGA определяет соответствующие преимущества каждой из них:

– ASIC–технология позволяет достичь конечного результата, который будет иметь наилучшие характеристики по производительности, размеру и энергопотреблению (что особенно важно в связи с бурным развитием, так называемых мобильных технологий - портативных устройств, питающихся от источников тока сравнительно низкой емкости);

– FPGA–технология обладает высокой степенью универсальности и гибкости – это возможность многократно и быстро перестраивать схему внутри FPGA микросхемы [19].

Однако применение FPGA имеет существенное преимущество, когда производство не носит массовый характер. Существенно большие затраты на разработку ASIC в сравнении с FPGA. Другие представители программируемой элементной базы, а именно микроконтроллеры и ЦПОС (цифровой процессор обработки сигналов) не рассматриваются, т.к. не позволяют полноценно реализовать параллельный подход к обработке сигналов навигационных космических аппаратов. Структура FPGA разработана именно для осуществления высокоскоростных параллельных вычислений, поэтому в работе в качестве элементной базы выбор сделан в пользу этой платформы.

Выводы по главе 1

1. Произведен анализ глобальной навигационной спутниковой системы и анализ структуры системы безопасности на основе глобальной навигационной системы GPS/ГЛОНАСС.

2. Рассмотрены методы и принципы определения координат и поиска сигналов в глобальной навигационной спутниковой системе. Рассмотрен дифференциальный режим DGPS.

3. Проведен анализ метода реализации навигационных устройств на программируемой элементной базе для подвижных объектов.

2 .1 Источники ошибок измерений спутниковой навигации

При отработке методов высокоточных спутниковых измерений возникает необходимость тщательного исследования влияний всех возможных источников ошибок выполняемых измерений, особенностей их проявления и обоснования методов их учета. В зависимости от характера воздействия отмеченных источников возникающие при этом ошибки подразделяются на две основные труппы: систематические погрешности, которые применительно к спутниковым измерениям получили название смещений, и погрешности случайного характера, которые часто отождествляют с понятием «шум».

Природа ошибок измерений спутниковой навигации различна. Ионосферные и атмосферные задержки вызваны тем, что поскольку спутниковый сигнал проходит через ионосферу, его прохождение может быть замедлено, эффект, подобный преломлению луча света, проходящего через стекло. Эти атмосферные задержки могут привести к ошибке в вычислении дальности, поскольку воздействуют на скорость сигнала. (Свет имеет постоянную скорость только в вакууме). Ионосфера не вызывает постоянной задержки сигнала. Есть несколько факторов, которые оказывают влияние на величину задержки, вызванной ионосферой.

Ошибки часов спутников и приемника возникают даже притом, что они очень точны (ошибка приблизительно 3 наносекунды), они иногда слегка уходят вперед или назад, что вызывает небольшие ошибки, воздействующие на точность определения координат. Также неточности спутниковых измерений возникают из-за переотражения. Переотражение происходит, когда антенна приемника установлена рядом с большой отражающей поверхностью типа озера или здания. Спутниковый сигнал не достигает антенны по прямой, а сначала попадает на близлежащий объект. В результате на антенну попадает отраженный сигнал, что образует ложное измерение. Переотражение может быть уменьшено с помощью специальных GPS антенн с встроенным защитным экраном (круглый, металлический диск приблизительно 50 см в диаметре), который предотвращают прием низко распространяющихся сигналов.

Шифрование кодовых данных, подобно S/A, является намеренным с целью препятствовать доступу к Р-кодовой части сигнала GPS гражданским лицам и неприятелю и, следовательно, вынудить их использовать C/A код, к которому применен S/A. A-S шифрует Р-код в результате чего получается сигнал, называемый Y-кодом. Только пользователи, имеющие армейские GPS приемники (США и их союзники) могут расшифровывать Y–код. Армейские приемники более точны, потому что они не используют C/A код для вычисления времени прохождения сигнала от спутника до приемника, для этого они используют Р–код. Несущая модулируется Р-кодом с частотой 10.23 Гц и C/A кодом с частотой 1.023 Гц. Следовательно, с помощью Р–кода дальности могут быть вычислены значительно точнее (в 10 раз), поскольку этот код генерируется 10 раз в секунду, а C/A код один раз в секунду. Р–код часто подвергается шифрованию (A-S). Это означает, что только военные, снабженные специальными GPS приемниками, могут считывать этот зашифрованный Р–код (также называемый Y–кодом). По этим причинам, пользователи военных GPS приемников обычно получают координаты с точностью около 5 м, а гражданские пользователи сопоставимых GPS приемников получат координаты с точностью лишь 15 – 100 м.

Избирательный доступ – это процесс воздействия на GPS сигнал Министерством обороны США. Предназначен он для того, чтобы частные лица и недружелюбные иностранцы не пользовались полной точностью GPS. Воплощается воздействием на спутниковые часы техникой известной как «добавление псевдослучайного сигнала», который слегка изменяет время. К тому же передаваемые эфемериды (или траектория движения спутника) слегка отличаться от той, что в действительности. Конечный результат состоит в снижении точности определения координат. Стоит отметить, что S/A воздействует на гражданских потребителей, использующих один GPS приемник, для получения автономного положения. На потребителей использующих дифференциальные измерения S/A существенно не воздействуют. В августе 2000 правительство США отключило S/A.

Неоптимальное взаимное расположение наблюдаемых спутников или геометрическое снижение точности (GDoP) – мера строгости спутниковой геометрии, использующаяся в области систем глобального позиционирования для параметрического описания геометрического взаиморасположения спутников относительно антенны приемника. В зависимости от взаимного расположения спутников на небосводе геометрические соотношения, которыми характеризуется это расположение, могут многократно увеличивать или уменьшать все неопределенности.

Геометрический фактор снижения точности GDoP.

Как правило, при вычислении координат учитываются следующие стандартные факторы снижения точности:

– горизонтальный фактор снижения точности (HDOP) – показывает степень влияния точности определения горизонтали на погрешность вычисления координат;

– фактор снижения точности определения положения (PDOP) – это безразмерный показатель, который описывает, как влияет на точность определения координат погрешность псевдодальности;

– относительный фактор снижения точности (RDOP) – по сути равен фактору снижения точности, нормализованному на период, составляющий 60 с;

– временной фактор снижения точности (TDOP) – описывает степень влияния погрешности показаний часов на точность определения координат;

– вертикальный фактор снижения точности (VDOP) – показывает степень влияния погрешности в вертикальной плоскости на точность определения координат;

– геометрический фактор снижения точности (GDOP) – говорит о степени влияния погрешностей псевдодальности (последняя характеризует меру удаленности потребителя от GPS–спутника). Зависит от положения спутника относительно GPS–приемника и от смещения показания GPS–часов. Различие значений псевдодальности и фактической дальности связано со смещением показаний часов GPS–спутника и потребителя, а также с задержками распространения и другими ошибками.

Точностные характеристики навигационных спутниковых систем определяются уровнем основных ошибок измерений и геометрическим расположением используемых спутников и потребителя. Геометрический фактор представляет собой коэффициент пересчета единичной погрешности измерения радионавигационного параметра в погрешность определения соответствующего параметра. В понятие геометрического фактора можно вкладывать разный смысл. Так, например, если оценивается точность пространственного (трехмерного) местоопределения, то речь идет о геометрическом факторе модуля вектора в пространстве, обозначаемым Гп. При оценке точности двумерного (горизонтального) местоопределения речь идет о геометрическом факторе модуля вектора в горизонтальной плоскости Гг, а при оценке точности только высоты о геометрическом факторе высоты Гв. Для оценки точности временного параметра говорят о геометрическом факторе времени Гт. При оценке точности четырехмерного пространственно временного вектора используют геометрический фактор Гч. Часто вместо термина «геометрический фактор» применяется обозначение. Это связано с тем, что по определению геометрический фактор означает, во сколько раз происходит уменьшение точности измерений при оценке того или иного параметра. Для четырехмерного геометрического фактора Гч. Используется обозначение GDOP (Geometrical DOP – означает учет всех составляющих четырехмерного вектора). - геометрическому фактору Гп соответствует PDOP (Position DOP означает учет составляющих вектора положения в пространстве);

– геометрическому фактору Гг соответствует HDOP (Horizontal DOP означает учет составляющих вектора положения в горизонтальной плоскости);

– геометрическому фактору высоты Гв соответствует VDOP (Vertical DOP);

– геометрическому фактору времени Гт соответствует TDOP (Time DOP).

GDOP (геометрическое снижение точности – термин, использующийся в системах спутниковой навигации для описания силы геометрического взаиморасположения спутников друг относительно друга. Когда спутники в области видимости находятся слишком близко друг к другу говорят о «слабой» геометрии расположения (высоком значении GDOP), и, наоборот, при достаточной удаленности геометрию считают «сильной» (низкое значение GDOP). Термин может применяться не только в спутниковом позиционировании, но и в других системах локации, включающим другие, географически разнесенные станции.

Геометрическое снижение точности (GDOP) – мера строгости спутниковой геометрии и связано с расположением спутников на небесной сфере. DOP может усилить воздействие ошибок определения координат спутника. Принцип может быть лучше проиллюстрирован схемами на рисунках 2.1 и 2.2 [11].

Рисунок 2.1 – Низкая неопределенность положения при «сильной» геометрии

Рисунок 2.2 – Высокая неопределенность положения при «слабой» геометрии

В случае, когда спутники расположены на небесной сфере достаточно широко («сильная» геометрия), искомое положение может находиться в пределах заштрихованной области (рисунок 2.1), и границы возможной ошибки малы. Иными словами, чем больше угол между направлениями на спутники, тем точнее местоопределение.

Когда спутники в области видимости находятся слишком близко друг другу («слабая» геометрия), размер заштрихованной увеличивается, что увеличивает неопределенность положения (рисунок 2.2).

На рисунке 2.1 передатчики расположены на большом расстоянии друг от друга, давая относительно небольшую определяемую область, в которой с некоторой вероятностью может находиться приемник. На рисунке 2.2 передатчики расположены ближе друг к другу, что в результате дает значительно большую область неопределенности.

Суть в том, что в зависимости от взаимного расположения спутников на небосводе геометрические соотношения, которыми характеризуется это расположение, могут многократно увеличивать или уменьшать все неопределенности, о которых мы только что говорили. Геометрический фактор снижения точности является индикатором надежности представления точности GPS позиционирования. Мы представляли наше местоположение относительно спутников в виде окружностей, центры которых совмещены со спутниками. А когда мы знаем, что каждое измерение содержит в себе и небольшую неопределенность, нам следует эти четкие окружности вообразить размытыми.

Наличие областей неопределенности означает, что мы не можем больше считать, что находимся в четко определенной точке. Можно сказать лишь, что мы где-то внутри этой суммарной области неопределенности.

В таблице 2.1 представлено описание значений GDOP – индикатора точности спутниковой навигации [12].

Таблица 2.1 – Описание значений GDoP

Геометрия спутников становится особенно важной при GPS–приемника в автомобиле, среди высоких зданий, в горах или в глубоких ущельях. Если сигналы от некоторых спутников оказываются экранированы, то точность определения местоположения будет зависеть от оставшихся «видимыми» спутников (а от их количества – возможность провести расчеты вообще). Чем большая часть неба заслонена искусственными или естественными предметами, тем более сложно определить положение. Хорошие модели GPS-приемников показывают не только сколько спутников находятся в зоне видимости, но и где они расположены на небе (направление и высоту над горизонтом) для того, чтобы Вы могли определить, не экранируется ли сигнал от данного спутника.

В зависимости от угла между направлениями на спутники область пересечения размытых окружностей (область неопределенности местоположения) может быть либо аккуратным небольшим квадратиком, либо сильно растянутым и неправильным четырехугольником. Проще говоря, чем больше угол между направлениями на спутники, тем точнее местоопределение.

Распространение радиоволн в атмосфере.

Немало важным остается вопрос распространения электромагнитных волн в земной атмосфере: тропосфере и ионосфере. Эти две среды являются принципиально разными с точки зрения взаимодействия с распространяющимися через них радиоволнами, поскольку с достаточной для практики точностью тропосферу можно считать нейтральной, в то время как ионосфера является электрически заряженной средой.

При прохождении сигнала через атмосферу содержащую водяной пар, возникает задержка радиосигнала, описанная выражением 2.1 и равная:

где – задержка радиосигнала в водяном паре при вертикальном распространении, м,

– отображающая функция, зависящая от угла места навигационного спутника.

Для расчета задержки сигнала при вертикальном распространении, обусловленной наличием водяного пара в атмосфере, необходимо интеграл представить в виде выражения 2.2:

где – взвешенное значение температуры воздуха, К.

Поскольку интегральное содержание водяного пара в столбе воздуха определяется выражением , то получается выражение 2.3:

Задержка радиосигнала во влажном воздухе зависит в первую очередь от значений интегрального содержания водяного пара (0.6 мм/кг/м2) и в меньшей мере от приземного значения температуры воздуха (0.5 мм/К) [13].

2 .2 Вычисление параметров пространственной ориентации

К параметрам пространственной ориентации относится тройка углов: угол крена, курсовой угол и угол тангажа. Определение пространственных координат требуется, как для автономного полета, так и дистанционно управляемого полета. Кроме того, если беспилотный летательный аппарат используется в качестве обнаружителя, например, источника радиоизлучения, то точность определения источника излучения напрямую зависит от точности определения пространственных координат. Далее будет рассмотрено построение модели алгоритма определения пространственной ориентации с целью получения оценок величины среднеквадратического отклонения найденных координат от их реальных значений. Основной причиной возникновения отклонения оценок от реальных значений являются ошибки в определении разности фаз, связанные с погрешностью определения момента прихода сигнала. Эти ошибки выражаются в виде среднеквадратичного отклонения разности фаз после обнаружителя [15].

Определенное с помощью модели требуемое число НКА соответствует числу требуемых каналов приема или же каналов обнаружителя.

Суть алгоритма заключается в сравнении полученных разностей фаз между элементами антенной решетки с эталонными разностями фаз , получаемыми заранее. Для этого кроме исходных координат антенн используются азимут и склонение спутника, чей сигнал принимается в данный момент.

Рассмотрим процесс определения эталонной разности фаз. В реальных условиях эти разности могут быть определены непосредственно на борту исследуемого объекта, но в рамках модели можно поступить следующим образом:

1. Находим разность координат между каждой парой элементов антенной решетки.

2. Используя матрицы поворота в пространстве, перебираем все возможные комбинации углов тангажа, крена и курсового. Таким образом, мы получаем все возможные значения пространственных координат.

3. По полученным вспомогательным данным, а также координатным углам навигационного космического аппарата находим искомые эталонные разности фаз, выражение (2.1).

где – склонение НКА,

– азимут НКА,

– вектор разностных координат антенной решетки для каждой пары ее элементов.

1. Совместная обработка данных разности фаз для заданного числа используемых НКА, заключающаяся в суммировании R из выражения (2.2) для всех используемых НКА .

1. Максимальное значение радиуса R – точка будет соответствовать полученной оценке пространственных координат.

На рисунке 2.3 представлена иллюстрация, показывающая систему координат, привязанную к объекту.

Рисунок 2.3 – Система координат, связанная с объектом

В качестве объекта будем рассматривать беспилотный летательный аппарат (БЛПА). Ось аппликат направлена перпендикулярно к горизонтальной плоскости, в которой расположена оставшаяся пара осей. Обозначение АНТ с цифровым индексом условно показывает расположение антенн на корпусе. Также на рисунке приведены углы, характеризующие положение навигационного космического аппарата (НКА) – азимут и склонение.

Чтобы не перегружать рисунок, обозначение углов пространственной ориентации было опущено. Однако, принимая во внимание вышесказанное, а также то, что ось Y соответствует направлению движения беспилотного летательного объекта, нетрудно установить, что курсовой угол – угол между осью Y и направлением на север, т.е. поворот во круг оси Z; угол крена – угол поворота вокруг оси Y, это угол между осью Х и горизонтальной плоскостью; тангаж – угол поворота относительно оси X, это угол между осью Y и горизонтальной плоскостью [15].

Блок-схема алгоритма вычисления параметров пространственной
ориентации.

В приложении А приводится блок-схема рассмотренного алгоритма, который наглядно иллюстрирует, каким образом алгоритм вычисления параметров пространственной ориентации реализуется с помощью языков программирования, например, Matlab, и позволяет проследить связь между этапами алгоритма.

Пример алгоритма вычисления параметров пространствнной ориентации иллюстрируется приведенным ниже кодом, представленным в листинге 2.1 [14].

Так в случае с языком Matlab блоки условия с последующими блоками действия, в которых определяется переход к следующему значению угла, переходят в три вложенных цикла for c условием остановки. А оставшиеся блоки условия выражаются в виде конструции if-else.

Описанный выше алгоритм используется для программирования на языке Matlab и описывает модель для проведения необходимых исследований.

В Приложении Б приводится реализация модели в среде Matlab. А результаты моделирования в виде графиков поверхностей приводятся на рисунках 2.4, 2.5.

Рисунок 2.4 – Зависимость значения функции R от углов тангажа и крена при фиксированном курсовом угле

Рисунок 2.4 соответствует описанной ранее функции R. По двум осям отложены значения углов тангажа и крена соответственно. Значения функции нормированы к максимуму для большей наглядности.

Из рисунка видно, что различить максимум, соответствующий пространственным координатам невозможно. Все пики имеют примерно одинаковую высоту. Однако, набирая статистику от нескольких НКА и суммируя соответствующие им функции R, можно добиться появления ярко выраженного пика. Пример представлен на рисунке 10.

Рисунок 2.4 – Зависимость значения функции RSUM от углов тангажа и крена при фиксированном курсовом угле

Получив функцию RSUM, можно приступить к вычислению среднеквадратического отклонения (СКО) угловых координат в зависимости от среднеквадратического отклонения разности фаз.

Результаты для трех углов, соответствующих положению беспилотного летательного аппарата в пространстве приведены на рисунках 2.5, 2.6 и 2.7 соответственно.

Рисунок 2.5 – Зависимость СКО оценки курсового угла в зависимости от СКО ошибки в определении разности фаз

Рисунок 2.6 – Зависимость СКО оценки угла крена в зависимости от СКО

ошибки в определении разности фаз

Рисунок 2.7 – Зависимость СКО оценки угла тангажа в зависимости от СКО ошибки в определении разности фаз

На каждом рисунке построены графики для числа НКА от 4 до 9. По мере увеличения числа НКА графики начинают сливаться. Более наглядным будет график, приведенный на рисунке 14. На этом рисунке построены зависимости СКО оценки пространственных координат от числа НКА. Для построения этих графиков был выполнен ряд испытаний, а результаты усреднены.

На рисунке 2.8 приведены зависимости, иллюстрирующие результаты моделирования, из которых видно, что среднеквадратическое отклонение определения пространственных координат уменьшается по мере роста числа навигационных космических аппаратов, но существенное уменьшение прекращается, начиная с области 6–8 навигационных космических аппаратов. Дальнейшие результаты приведены для выбранного числа навигационных космических аппаратов, равного 7. При реализации алгоритма на программируемой элементной базе число навигационных космических аппаратов соответствует числу логических каналов, это значит, что требуемые ресурсы FPGA растут с увеличением числа навигационных космических аппаратов. В тоже время, чем меньше среднеквадратическое отклонение оценки пространственных координат, тем точнее будут проводимые в дальнейшем измерения, опирающиеся на полученные данные. Таким образом, соблюдая компромисс между величиной погрешности требуемыми ресурсами, делаем вывод, что достаточно приема 7 навигационных космических аппаратов.

Рисунок 2.8 – Зависимость СКО оценки пространственных координат от числа

навигационных космических аппаратов

Результаты моделирования получены стационарным образом при задании одного и того же исходного положения навигационного космического аппарата. Тем самым полученные результаты определяются исключительно взаимным расположением исследуемого подвижного объекта и созвездия спутников, а не конкретными значениями пространственных координат. Перебор углов пространственной ориентации исследуемого подвижного объекта приводит к перебору взаимных положений, при этом изменение координат спутника влияет только на порядок этого перебора. Характеры зависимостей при этом сохраняются, возможны лишь незначительные отклонения полученных оценок.

2 .3 Методы решения навигационных задач

Определение координат приемника производится одним из трех методов:

• абсолютным,

• дифференциальным

• относительным.

При абсолютном методе положение вычисляется одним приемником, для которого отыскиваются его координаты в системе связанной со станциями наблюдения (управляющий сегмент) и самими спутниками.

Для применения дифференциального и относительного методов необходимо наличие как минимум двух приемников, при том что второй приемник является опорной станцией и должен иметь достаточно хорошо вычисленные координаты. В дифференциальном методе по координатам, вычисленным на опорной станции составляются поправки для координат целевого пункта. Это позволяет осуществлять расчет координат в реальном времени с точностью лучшей чем абсолютный метод. В относительном методе координаты для целевого пункта вычисляются параллельно с координатами для опорного пункта. Объектом измерения выступает базовая линия между двумя пунктами. Этот повышает точность измерений, но лишает оперативности и возможности измерений в реальном времени.

Все три метода могут использоваться как для оперативного получения координат приемника, так и для получения данных для постобработки. Так же, все три метода могут применяться как для определения положения статических объектов, так и подвижных (кинетическая съемка) объектов.

Наблюдения по кодовым псевдодальностям дают ошибку определения координат порядка метров и даже десятков метров. Подобные измерения по фазам могут иметь сантиметровый, и даже миллиметровый уровень точности. Как говорилось выше абсолютный метод имеет наибольшие ошибки вычисления. Одна из причин этого – применение бортовых координат спутников, которые сами по себе имеют ошибку порядка метра и более. Для корректного применения абсолютного метода используются точные апосториальные эфемериды, которые появляются на ресурсах с большой задержкой. Хотя, за последние годы эта задержка сильно сократилась с трех - четырех дней до двух. Подробные алгоритмы расчета положения объектов по навигационным измерениям описаны в литературном источнике [31]. Здесь же будут приведены лишь описание основных принципов работы этих алгоритмов.

Абсолютный метод

Применение абсолютного метода сводится к получению значения дальности до спутника из выражения 2.3:

где – значение псевдодальности, получаемое от приемника, м,

– индекс, относящийся к спутнику,

– индекс, относящийся к пункту приема,

– расхождение шкал приемника и спутника, м,

– тропосферная задержка, м,

– ионная задержка, м,

– задержка при прохождении радиотракта в спутнике, м,

– задержка при прохождении радиотракта в приемнике, м,

– задержка, возникающая по причине многопутности, м,

– случайный ошибки, м,

– расстояние между спутником в момент отправки сообщения и приемником в момент получения сообщения, м.

Расстояние между спутником в момент отправки сообщения и приемником в момент получения сообщения, вычисляется через разницу радиус-векторов из выражения 2.4:

Решение этого уравнения возможно лишь при условии получения всех поправок, составляющих разницу между истинным расстоянием и псевдодальностью, измеренной приемником по времени прохождения сигнала. Отклонение шкалы спутника может быть получено через коэффициенты ухода шкалы, которые приходят в навигационном сообщении. Многопутность, как правило, в расчетах не может быть точно установлена, поэтому полагается, что она отсутствует. Задержки в прохождение сигнала по излучающим и принимающим трактам приемника и спутника устанавливаются путем калибровок, либо также игнорируются, считаясь шумом. Координаты спутника вычисляются по координатам, полученным из навигационного сообщения, либо из сторонних источников и рассчитываются на момент отправки сигнала. Для ГЛОНАСС расчет производится путем интегрирования, для GPS – аналитически. После этого координаты корректируются с учетом поворота Земли за время прохождения сигнала. Это осуществляется перемножением вектора координат на матрицу поворота [1].

Краеугольным камнем этого подхода является учет тропосферной и ионосферной задержек – и . Эти две величины подвержены сильным изменениям, не зависящим от внутреннего состояния ГНСС, то есть не могут быть полностью высчитаны без применения внешних источников. Для их учета применяются ряд ионосферных и тропосферных моделей. Эти модели будут рассмотрены в следующей главе. Здесь же следует заметить, что в уравнение абсолютного метода они являются членами одного порядка с расстоянием и псевдодальностью и могут оказывать большое влияние на расчет местоположения приемника.

Разрешение всех поправок и добавление их в уравнение псевдодальности в сухом остатке дает лишь четыре неизвестные: три координаты местоположения станции и расхождение временной шкалы станции. Эти неизвестные находятся составлением системы уравнений псевдодальностей до нескольких наблюдаемых одновременно спутников [32].

Дифференциальный метод

В дифференциальном методе определения координат используются минимум два приемника. Один из них располагается в пункте, называемом опорной станцией. Его координаты известны заранее с высокой точностью. При дальнейшей работе полагается, что ошибки определения координат на опорной станции и на целевом пункте одинаковы и, измерив их величину на опорной станции, можно скорректировать измеренное положение целевой станции. Как правило, аппаратура на опорной станции, работая в обычном режиме, принимает навигационную информацию от спутников и пытается рассчитать по ней свое положение. После этого, сравнив его с точными координатами известными заранее, она вычисляет значение поправок к определению местоположения и передает их на целевую станцию. Передача может осуществляться как оперативно по сетям связи (реал-тайм обработка), так и позже на компьютер, осуществляющий обработку (пост-тайм обработка) [6].

Тот факт, что расхождение в величинах поправок сильно меняется по мере удаления от одной опорной станции, приводит к появлению методов измерения поправок по сети опорных станций, что позволяет добиться более равномерного распределения ошибок расчета поправок.

Такой подход к поправкам навигационных измерений требует более детального рассмотрения изменений в пространстве и времени отдельных источников ошибок.

Ошибка часов спутника является меленькой величиной (до 10 нс) и очень медленно изменяется в течении часов. Она практически не зависит от расстояния между опорной и целевой станциями.

Ошибка координат спутника, как правило, умещается в порядок 2 метров и также медленно изменяется с течением времени. Для навигационных спутников, находящихся на расстоянии 20000–30000 км от приемника, отклонение от положения в сторону перпендикулярную направлению от спутника до приемника будет иметь малую угловую величину и не окажет особого значения на расчет положения. Более серьезные ошибки возникают при отклонении вдоль топоцентрического радиус-вектора. При расстояниях до 100 км величина нескомпенсированной ошибки может составить 5 см.

Ионосферная задержка зависит от полного ионного содержания TEC на пути распространения сигнала. TEC же, в свою очередь, является сильно изменчивой величиной. Остаточная ошибка после проведения дифференциальной коррекции может иметь порядок 10–20 см для невозмущенной ионосферы и порядок 1–2 м для возмущенной при расстояниях между приемниками до 100 км.

Тропосферная задержка зависит от плотности и состава воздуха на пути распространения. Кроме того, она сильно зависит от изменчивости водяного пара. Даже расположение приемников на одной высоте, но на расстоянии 10 км друг от друга может привести к ошибкам порядка 10–20 см. При сильной разнице в метеоусловиях на пунктах измерения, а также при большой разнице в высотах тропосферная задержка может иметь очень большие значения. По этой причине рекомендуется вычислять тропосферную задержку раздельно для опорной и для целевой позиции. Многопутность и шум приемника являются некоррелированными ошибками, и их передача с опорной станции на целевую лишь приведет к ухудшению навигационных измерений. По этой причине эти ошибки стараются минимизировать еще до передачи на целевую станцию.

Относительное позиционирование

Метод относительного позиционирования применяется для расчета расстояния между двумя пунктами, называемого вектором базовой линии, либо базовой линией. Расстояние вычисляется после получения приблизительных координат двух точек. Оно выражается как вектор разности радиус векторов двух точек. Могут применяться двойные и тройные разности [33].

Выводы по главе 2

1. Рассмотрены Источники ошибок измерений спутниковой навигации, факторы, влияющие на снижение точностных характеристик. Детально рассмотрен геометрический фактор снижения точности позиционирования навигационного космического аппарата. Исследовано распространение радиоволн в атмосфере и влияние этих показателей на точность позиционирования навигационного космического аппарата.

2. Детально рассмотрен алгоритм вычисления параметров пространственной ориентации, представлена блок-схема алгоритма и проведены результаты моделирования в системе Matlab.

3. Рассмотрены методы решения навигационных задач.

3 .1 Построение алгоритма обнаружителя сигналов спутника

Одним из основных элементов пользовательского интерфейса является обнаружитель сигналов навигационной космической аппаратуры системы GPS. Обнаружение требуется в каждом логическом канале, поэтому реализация обнаружителя во многом будет играть определяющую роль в определении требуемых ресурсов FPGA.

В качестве обнаружителя могут выступать, как коррелятор, так и согласованный фильтр (СФ). В обоих случаях качество работы обнаружителя будет зависеть от величины ошибки в определении момента прихода полезного сигнала, однако при использовании СФ эта процедура упрощается т.к. максимум выходного напряжения СФ, соответствующий моменту прихода, всегда с некоторой задержкой будет присутствовать на выходе.

Реализация согласованного фильтра предполагает осуществление свертки входного сигнала с инвертированной копией искомого сигнала. Свертка может выполняться как напрямую, так и методом быстрой свертки. Метод быстрой свертки заключается в том, что последовательности – аргументы свертки подвергаются сначала быстрому преобразованию Фурье, затем перемножаются, а конечный результат получается путем обратного преобразования произведения.

При этом метод быстрой линейно свертки предполагает меньшую вычислительную сложность по сравнению с прямым подходом в случае, если число значений, подлежащих свертке, достаточно велико. В этом случае уменьшается и требование к ресурсам FPGA, что немало важно.

Ниже сравнивается число умножений, требуемых для выполнения свертки с помощью прямого и быстрого методов, выбранное в качестве меры их относительной вычислительной эффективности.

Известно, что для выполнения линейной свертки двух последовательностей длины требуется произвести умножений. Выполнение той же линейной свертки, но с помощью быстрого метода потребует число умножений .

Ниже приведена таблица 3.1, представляющая число требуемых умножений в зависимости от .

Таблица 3.1 – Число действительных умножений, требуемых для выполнения свертки двух N–точечных последовательностей.

Из таблицы 3.1 видно, что начиная с N=128, выгоднее использовать быструю свертку, и с дальнейшим ростом размерности преимущество в вычислительных затратах становится все более заметным. С учетом того, что длина C\A-кода равна 1023, а на каждый элемент кода берется два отсчета, требуется свертка двух последовательностей длины 2046. Но для реализации быстрого метода длина должна быть кратна степени двойки. Дополнение нулями в данном случае исказит результат, поэтому следует взять в качестве исходной последовательности – последовательность отсчетов сигнала длиной = 4096, а опорную последовательность с дополнить нулями до этой же длительности.

Работа обнаружителя начинается с накопления 4096 отсчетов входного сигнала. В результате быстрой свертки будут получены 1 отсчетов, т.е. 2051 отсчет, соответствующий линейной свертке. После завершения расчета самые старые 2051 отсчета отбрасываются и заменяются очередными отсчетами сигнала, накопленными за время вычисления.

3 .2 Построение модели обнаружителя сигналов навигационной спутниковой системы GPS и его программная реализация в соответствии с построенным алгоритмом

Для качественной проверки работы обнаружителя, реализованного непосредственно на FPGA, необходимо создать его модель в среде Matlab. Результат моделирования процесса обнаружения необходимо сравнить с результатами тестирования реально созданного обнаружителя на FPGA, при подаче на FPGA генератора реального сигнала, построенного на основе C/A–кода. В качестве тестового воздействия в модели используется тот же в вариант C/A–кода.

Выбранный для проверки C/A–код преобразуется из бинарного вида в биполярный, т.е. «1» переходит в «-1», а «0» в «1». Полученную таким образом последовательность будем использовать в качестве вещественной компоненты комплексной огибающей сигнала.

Для примера приведены графики последовательности в бинарном виде на рисунке 3.1 и в биполярном виде на рисунке 3.2.

Рисунок 3.1 – Бинарный вид C/A–кода

Рисунок 3.2 – Биполярный вид C/A–кода

Сама модель таким образом состоит из следующих частей – схема формирования тестового сигнала, непосредственно сам обнаружитель и модуль, формирующий вывод результатов в виде графиков. Структурная схема приведена на рисунке 3.3.

Рисунок 3.3 – Структурная схема тестовой модели

На рисунке 3.4 приводится функциональная схема блока, отвечающего за формирование тестового воздействия. Sвх соответствует входному сигналу, представляющему смесь полезного сигнала с шумом. Для теста выбран Гауссовский шум, как наиболее характерный для спутниковых каналов связи, характеризущийся равномерной, то есть одинаковой на всех частотах спектральной плотностью мощности, нормально распределенными временными значениями и аддитивным способом воздействия на сигнал [14]. Sоп соответствует формируемому в обнаружителе опорному сигналу, фактически должен входить в состав обнаружителя, но для наглядности вынесен именно в данный блок.

Рисунок 3.4 – Функциональная схема формирования тестового воздействия

Обнаружитель С\А–кода, как было сказано выше реализуется в виде согласованного фильтра и включает в свой состав решающее устройство, принимающее решении об обнаружении. Функциональная схема обнаружителя приведена на рисунке 3.5.

Рисунок 3.5 – Функциональная схема обнаружителя

На рисунке 3.6 приведена блок-схема данного алгоритма.

Рисунок 3.6 – Блок-схема алгоритма обнаружителя в среде Matlab

Полученная модель использована для тестирования прошивки, полученной для FPGA. Критериями сравнения являются ширина пика, соответствующего максимуму, а также отношение значения этого пика к уровню окружающих значений.

На вход фильтра подается некоторая реализация, представляющая сумму биполярного С\А–кода и аддитивного Гауссовского шума в полосе сигнала.

Фильтр осуществляет быструю свертку поступившей реализации с псевдослучайной последовательностью. Затем находится пик результата быстрой свертки и принимается решение о принятой реализации: содержит или нет, она исходную псевдослучайную последовательность.

Входная реализация процесса задается как периодически повторяющаяся псевдослучайная последовательность с шумом. Результат работы программы продемонстрирован на рисунке 3.7. Приведены иллюстрации для ситуаций, когда:

• С\А–коды приходящего и опорного сигналов совпадают,

• С\А–коды приходящего и опорного сигналов не совпадают.

Рисунок 3.7 – Результат моделирования обнаружителя в среде Matlab

Прежде чем приступить к реализации модели обнаружителя на языке VHDL в среде HDLdesigner, необходимо определится со структурой обнаружителя. Для этого в первую очередь необходимо определить механизм поиска по доплеровской добавке к частоте и кодовому смещению.

Можно представить некое пространство, имеющее свою координатную сетку, характеризующее эти параметры. Иллюстрация приведена на рисунке 3.9.

Рисунок 3.9 – Координатная сетка пространства D-F

Ось D соответствует кодовому сдвигу, а величина шага по ней определяется количеством отсчетов на один чип псевдослучайной последовательности. Как правило, выбирают либо 2, либо 4 отсчета на чип. Увеличение числа отсчетов до 4 позволяет достичь большей точности, но при этом увеличивает объем вычислений, что приведет либо к увеличению требуемого числа ресурсов, либо к увеличению затрачиваемого на расчеты времени. С учетом этого выбран вариант с 2-мя отсчетами на элемент кода. А чтобы сохранить точность, после превышения порога проводится дополнительный поиск в пределах 3-х чипов в обе стороны от найденной позиции.

Вторая ось (F) отвечает за доплеровскую добавку по частоте. Как правило, для пользовательского навигационного устройства эта величина не превышает ±5 кГц. Для обеспечения достаточной точности выбирается шаг 100 Гц.

Переходим к выбору схемы перебора этих параметров. В случае отказа от использования параллельного подхода общее время перебора всей сетки используем выражение 3.1

где M – число чипов в последовательности,

N – число возможных сдвигов по частоте,

TC – время на обработку одного чипа.

С учетом двух отсчетов на чип общее время увеличится в 4 раза. Схема перебора с последовательно-параллельной обработкой различны смещений приводит к уменьшению Т в К раз согласно выражению 3.2.

где К – кол-во одновременно обрабатываемых чипов.

В случае использования схемы с диапазонным полосовым фильтром (ДПФ) в качестве «гетеродина» параметр К будет соответствовать длине ДПФ.

С учетом создания требований к гибкости конечного устройства предпочтение отдается первому варианту схемы, т.к. изменение длины ДПФ во втором случае жестко связано с сеткой доплеровских смещений. Уменьшение длины ДПФ приведет к увеличению шага и потери точности, а увеличение – к чрезмерному уменьшению шага, а значит и повысит время, необходимое для полного сканирования.

Кроме того, длина ПСП является достаточной для получения преимущества от применения так называемой быстрой свертки, основанной так же на ДПФ. Алгоритм быстрой свертки дает выигрыш по числу используемых операций для получения результата круговой свертки, с помощью которой может быть выражен результат перебора по всем возможным смещениям ПСП.

На рисунке 3.10 приведена принципиальная схема обнаружителя, полученная с помощью среды HDLdesigner.

Рисунок 3.10 – Принципиальная схема обнаружителя в среде HDLdesigner

При разработке в среде HDLdesigner для FFT, IFFT и комплексного умножения использовались готовые ядра от компании Xilinx. Они позволяют добиться требуемой функциональности с меньшими затратами ресурсов. Кроме того, с помощью синтезатора проведена следующая оценка требуемых ресурсов.

Результат оценки приведен в виде снимка экрана главного окна программы. Этот результат можно посмотреть на рисунке 3.11.

Без использования ядер, а также при отказе от использования метода быстрой свертки, потребление ресурсов возрастает на несколько порядков. Цифры приведены после двухэтапной оптимизации: с помощью синтезатора и вручную.

Полученные данные анализа требуемых ресурсов показывают, что для реализации ПНУ можно использовать FPGA фирмы Xilinx XSV5465TFFF или более старшие модели.

Рисунок 3.11 – Оценка использования ресурсов

В листинге 3.1 приводится код на языке VHDL, реализующие основные функции по управлению одним логическим каналом.

Первый этап работы обнаружителя заключается в накоплении двух периодов входной ПСП с учетом числа символов на чип. Затем наступает второй этап – непосредственно реализация быстрой свертки и обработка полученных результатов. После завершения, если необходимо происходит перестройка частоты на величину выбранного шага.

3 .3 Анализ полученных результатов

Результаты работы полученной реализации на FPGA сравнивались с описанной выше моделью в среде Matlab. На рисунке 3.12 приведены графики для обеих ситуаций:

а) результат, полученный для Matlab

б) результат работы реального обнаружителя, экспортированный для удобства в Matlab.

Для наглядности на обоих графиках увеличен масштаб. Внимание намеренно акцентировано на фрагментах, вблизи главного максимума.

Рисунок 3.12 – Оценка использования ресурсов

Из приведенных графиков видно, что ширина главного максимума совпадает, как и положения других характерных точек, а именно локальных экстремумов.

Небольшие различия в значениях вызваны целочисленным характером вычислений внутри FPGA и не превышают доли процента для главного максимума, так и для среднего уровня шумов.

Рекомендации по повышению точности спутниковых измерений.

Погрешности в спутниковых измерениях могут возникнуть в случае, когда приемник в области видимости находит малое количество спутников. Как было сказано ранее, для того, чтобы GPS-приемник мог определить трехмерные координаты и время, ему необходимо «видеть» как минимум 4 спутника. «Видимость» приемником спутников может быть осложнена рельефом местности, крупногабаритными городскими строениями, атмосферными осадками, антенна GPS приемника не может принимать сигнал со всех сторон из-за препятствий.

Единственное решение в повышении точности спутниковых измерений на данный момент – это наблюдение большего количества спутников. Возможность слежения за большим количеством спутников может помочь в такой ситуации и применение совмещенных приемников GPS/ГЛОНАСС может позволить достичь требуемой точности. Если мы получаем сигнал только из ограниченной области небесного пространства, значение GDOP будет большим, точность определения времени и координат объекта уменьшится. Новые технологии, используемые при создании приемников, позволяющие работать со слабыми сигналами GPS даже внутри зданий также позволят добиться хороших результатов.

Одной из таких технологий является применение дифференциального режима DGPS.

Дифференциальный режим DGPS используется для повышения точности GPS путем исключения атмосферных искажений сигнала на приемниках. Сигналы DGPS коррекции посылаются пользователям по радио. DGPS-приемник работает на средних частотах 283,5–325 кГц [17]. Передаваясь, сигналы на этих частотах отражаются от поверхности земли. Поэтому холмистая и горная местность обычно не влияет на прием сигнала. Однако в глубоких каньонах далеко от радиомаяка, где радиосигналы традиционно слабы, сигналы коррекции могут быть не приняты.

Точность определения местоположения с помощью GPS обычно составляет от 5 до 30 метров, чего явно недостаточно при проведении работ, требующих высокой точности определения координат. Система DGPS предназначена для повышения точности определения координат, обеспечивая получение GPS-приемником дополнительных дифференциальных поправок. Дифференциальный режим позволяет уменьшить неопределенности измерений до 0,25 м.

Вывод по главе 3

1. Выполнено построение алгоритма обнаружителя сигналов спутника. Проанализированы результаты применения различных методов свертки, для достижение наименьшей вычислительной сложности

2. Построена модель обнаружителя сигналов навигационной спутниковой системы GPS предложена его программная реализация в соответствии с построенным алгоритмом.

3. Проведен анализ результатов моделирования алгоритма обнаружителя сигналов. Описаны рекомендации по повышению точности спутниковых измерений.