1 Натуральные числа. Разряды и классы натуральных чисел

Для счёта предметов применяют натуральные числа. Любое натуральное число можно записать с помощью десяти цифр:

   
О,  1,  2,  3,  4,  5,  6,  7,  8,  9.     

Например: триста двадцать восемь - 328

пятьдесят тысяч четыреста двадцать один - 50421

Такую запись чисел называют десятичной.

Последовательность всех натуральных чисел называют натуральным рядом:

1,  2,  3,  4,  5,  6,  7,  8,  9,  10,  11,  12,  13,  14,  15,  16,  17,  18,  19,  20,  ...   

Самое маленькое натуральное число — единица (1). В натуральном ряду каждое следующее число на 1 больше предыдущего.

Натуральный ряд бесконечен, наибольшего числа в нем нет.

Значение цифры зависит от ее места в записи числа.

Например 375:

цифра 5 означает: 5 единиц, она на последнем месте в записи числа (в разряде единиц),
цифра 7 - десятки, она находится на предпоследнем месте (в разряде десятков),
цифра 3 - сотни, она стоит на третьем месте от конца (в разряде сотен) и т. д.

Цифра 0 означает отсутствие единиц данного разряда в десятичной записи числа. Она служит и для обозначения числа "нуль".

Это число означает "ни одного".

Помните! Нуль не относят к натуральным числам.

Если запись натурального числа состоит из одного знака — одной цифры, то его называют однозначным.

Например, числа 1, 5, 8 — однозначные.

Если запись числа состоит из двух знаков — двух цифр, то его называют двузначным.

числа 14, 33, 28, 95 — двузначные,
числа 386, 555, 951 — трехзначные,
числа 1346, 5787, 9999 — четырехзначные и т. д.

Разряды и классы  натуральных чисел

Для записи чисел используется ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ. В десятичной системе счисления пользуются единицами, десятками единиц, десятками десятков — сотнями и т. д.
Каждая новая единица счёта больше предыдущей ровно в 10 раз:

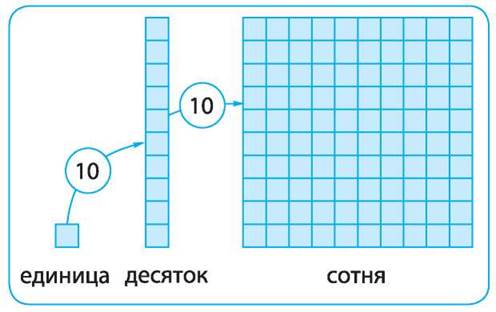
Десятичная система счисления — позиционная. В этой системе счисления значение каждой цифры в записи числа зависит от её позиции (места).

Позиция (место) цифры в записи числа называется разрядом. Самый младший разряд — ЕДИНИЦЫ. Затем следуют ДЕСЯТКИ, СОТНИ, ТЫСЯЧИ и т. д.

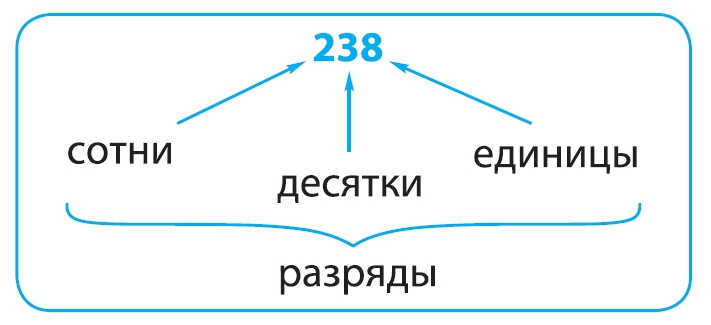
Каждые три разряда натуральных чисел образуют класс.

2 Сравнение натуральных чисел. Знаки "<" и ">"

Сравнение в жизни мы используем постоянно. Например, длинная дорога или короткая, высокий или низкий человек, много игрушек или мало, большая емкость или маленькая. Так, что же такое сравнение натуральных чисел?

Сравнение натуральных чисел – это определение какое из натуральных чисел больше, а какое меньше.

Способы сравнения натуральных чисел.

Рассмотрим натуральный ряд чисел.

1, 2, 3, 4, 5, 6, 7, 8, 9,10, 11, 12, 13, 14, 15, …

1) Всегда числа, стоящие справа в натуральном ряду больше чисел, стоящих слева.
Например, сравним числа 7 и 9. Число 9 стоит правее числа 7, следовательно, число 9 больше 7.

Единица, является самым маленьким натуральным числом.

Любое натуральное число больше нуля.

2) Всегда больше то натуральное число, у которого разрядов больше.

Сравним два числа 45 и 190. Сразу понятно, что число 190 больше числа 45. Мы сделали такой вывод потому, что число 190 является трехзначным числом, а 45 – двухзначным числом. У числа 190 есть разряд сотен, десятков и единиц, а у числа 45 только разряд десятков и единиц.

3) Если количество разрядов одинаково, то мы будем сравнивать величины цифр разрядов, начиная с высшего разряда (слева направо).
Например, сравним числа 478 и 399. Оба числа являются трехзначными, поэтому подробно рассмотрим высший разряд сотен. У первого числа 478 разряд сотен равен 4, а у второго числа 399 разряд сотен равен 3. Следовательно, первое число 478 больше второго числа 399, потому что 4 больше 3.

478 больше 399

Если высшие разряды одинаковые мы сравниваем следующий меньший разряд цифр.
Сравним числа 7890 и 7860. Начинаем сравнивать высший разряд единиц тысяч он у обоих чисел равен 7. Следующий разряд сотен, также равен у обоих чисел 8. А вот разряд десятков различен. У первого числа 7890 разряд десятков равен 9, а у второго числа 7860 равен 6. Далее делаем вывод, первое число 7890 больше 7860, потому что разряд десятков у первого числа больше чем у второго. Проще сказать, 9 больше 6.

7890 больше 7860

4) Если при сравнении все цифры разрядов двух натуральных чисел одинаковы, значит числа равны.
Например, сравним числа 4890765 и 4890765. Видно, что у обоих чисел все цифры разрядов одинаковы, следовательно, они равны.

4890765 равно 4890765

Неравенство и знаки неравенства.

Чтобы не писать словами больше, меньше или равно в математике придумали обозначения. Больше (>), меньше (<), равно (=). Например, 3 больше 2 математическая запись будет выглядеть так 3>2. Или 6 меньше 10, мы запишем как 6<10. 8 равно 8, запишем 8=8.

Выражения 3>2, 6<10 и 8=8 называются в математики неравенствами.

Такая запись 2<3<4 называется двойным неравенством.

3 Сложение и вычитание натуральных чисел

Сложение натуральных чисел

Арифметическая операция сложения чисел обозначается значком "плюс" (+).

A + B = C

• Натуральные числа А и В называются слагаемыми;
• Число С называется суммой чисел А и В или результатом сложения (поскольку А и В являются натуральными числами, то и число С всегда будет натуральным числом).

Свойства сложения натуральных чисел:

1. Переместительное свойство - от перестановки местами слагаемых сумма не изменяется:

   А+В = В+А = С;

2. Сочетательное свойство - отыскивая сумму трех слагаемых, не имеет значения в каком порядке производить суммирование слагаемых:

   A+B+C = (A+B)+C = A+(B+C)

3. Свойство нуля при сложении - при прибавлении к любому числу нуля, число не изменяется:

   А+0 = 0+А = А

Вычитание натуральных чисел

Арифметическая операция вычитания чисел обозначается значком "минус" (-).

A - B = C

• А - уменьшаемое;
• В - вычитаемое;
• С - разность.

Разностью чисел А и В называется такое число С, которое надо прибавить к вычитаемому, чтобы получить уменьшаемое:

A - B = C;
В + С = А.

Складываются и вычитаются натуральные числа поразрядно, начиная с самого младшего разряда:

 255 808
+
 308 012
 -------
 563 820

Если при сложении двух цифр какого-либо разряда получается число, большее 9, то в сумму записывается только цифра, обозначающая разряд единиц, а "единичка" переходит в следующий разряд. Например, в приведенном выше примере при суммировании 8 и 2 получается 10 - в сумму заисывается 0, а 1 переходит в разряд десятков: 0+1+1 = 2. При суммировании 5 и 8 получается 13, поэтому в сумму (в разряд единиц тысяч) записывается 3, а 1 переходит в разряд десятков тысяч: 5+0+1 = 6.

 355 808
-
 308 012
 -------
  47 796

Если при вычитании приходится вычитать в соответствующем разряде большую цифру из меньшей, меньшая цифра "заимствует" единицу старшего разряда. Например, в нашем примере, при вычитании 0-1 (разряд десятков) ноль "занимает" единичку у разряда сотен (у восьмерки, стоящей левее), и становится не нулем, а 10, таким образом, мы вычитаем 1 не из нуля, а из 10 (получаем 9); теперь при вычитании разряда сотен мы будем отнимать 0 не от 8, а от 7, поскольку восьмерка "отдала" одну десятку в младший разряд. Аналогичная ситуация при вычитании 8 из 5: пятерка "занимает" десятку у пятерки, стоящей левее, и становится 15, теперь мы отнимаем 8 от 15 и получаем 7, после этого мы вычитаем 0 уже не от пятерки, а от четверки. Если в самом старшем разряде получается ноль, он не пишется.

4 Умножение натуральных чисел. Свойства умножения

Умножая два натуральных числа, получаем результат, который производится при умножении однозначных натуральных чисел. Произведение чисел 6 и 3 приравнивается к сумме, состоящей из трех слагаемых, равных числу 6. Иначе это запишем: 6⋅3=6+6+6=18. Таким же образом получены все результаты умноженных однозначных натуральных чисел.

Таблица умножения:

Умножение трех и более количества чисел

Мы дали определение понятию умножения двух чисел. Теперь поговорим об умножении трех и более имеющихся чисел. Таким образом, в такой ситуации применимо сочетательное свойство умножения натуральных чисел.

Сочетательное свойство умножения показывает равнозначность двух произведений a⋅(b⋅c)

и (a⋅b)⋅c, где a, b и c могут быть любыми числами. Результат умножения данных чисел не будет зависеть от местоположения скобок. Поэтому чаще всего при произведении скобки отсутствуют, а запись имеет вид a⋅b⋅c

Данное выражение называют произведением трех чисел, причем все входящие в него числа – множители.

Сочетательное свойство умножения необходимо для того, чтобы легче было выявлять равные произведения. Это значит, что из приведенных (a⋅b)⋅(c⋅d), (a⋅(b⋅c))⋅d, ((a⋅b)⋅c)⋅d, a⋅(b⋅(c⋅d))

и a⋅((b⋅c)⋅d) можно сделать вывод, что они все равные. Положение скобок при умножении не играет роли. Это произведение может быть записано в виде a⋅b⋅c⋅d

Обычно скобки опускаются при умножении. Произведение нескольких трех и более чисел без скобок приводит к последовательной замене двух соседних множителей до получения необходимого результата. Скобки могут быть расставлены произвольно, так как итог произведения не изменится.

Если взять пять натуральных чисел и записать их в виде произведения, то получим 2⋅1⋅3⋅1⋅8

Имеется два основных способы решения.

Первый способ заключается в том, что два множителя слева будут последовательно заменяться произведением. Тогда получим, что 2⋅1⋅3⋅1⋅8=2⋅3⋅1⋅8

Так как 2⋅3=6, то 2⋅3⋅1⋅8=6⋅1⋅8. Далее имеем, что 6⋅1=6, тогда в итоге получим результат 6⋅8=48. Умножение пяти заданных чисел будет равняться 48. Этот способ записывается, как (((2⋅1)⋅3)⋅1)⋅8

Второй способ заключается в том, что скобки располагаются таким образом ((2⋅1)⋅3)⋅(1⋅8)

Имеем, что 2⋅1=2 и 1⋅8=8, то ((2⋅1)⋅3)⋅(1⋅8)=(2⋅3)⋅8. При 2⋅3 равном 6 получим, что (2⋅3)⋅8=6⋅8. В итоге получим, что 6⋅8=48. Отсюда следует, что 2⋅1⋅3⋅1⋅8=48

Порядок следования множителей не влияет на результат. Множители могут быть записаны в любом порядке. Это следует из свойств умножения натуральных чисел.

Свойства умножения

При решении различных задач применяют свойства умножения.

1. Переместительное: от перестановки мест множителей значение произведения не меняется.

2. Сочетательное: чтобы число умножить на произведение двух чисел, можно его сначала умножить на первый множитель, а затем полученное произведение умножить на второй.

3. Умножение на единицу: если число умножить на единицу, то число не изменится.

4. Умножение числа на нуль: если число умножить на нуль, то получится нуль.

Т. е., при умножении любого числа на нуль, получится нуль.

Примеры.

1.

2.

3.

4.

5. .

Все эти свойства удобно применять при решении различных примеров.

5 Квадрат и куб числа

Возведение числа в квадрат - это умножение числа на само себя.

Возведение числа в куб - это умножение числа на само себя дважды. Т.е. если квадрат числа умножить на число получим куб числа.

Квадраты натуральных чисел от одного до ста

Кубы натуральных чисел от одного до ста

6 Деление натуральных числел

Рассмотрим понятие деление на задаче:

В корзине лежало 12 яблок.  Шестеро детей разобрали яблоки. У каждого ребенка получилось одинаковое количество яблок. Сколько яблок у каждого ребенка?

Решение:
Нам нужно 12 яблок поделить на шестерых детей. Запишем математически задачу 12:6.
Или по-другому можно сказать. На какое число нужно умножить число 6, чтобы получилось число 12? Запишем в виде уравнения задачу. Количество яблок нам неизвестно, поэтому обозначим их за переменную x.

x⋅6=12

Чтобы найти неизвестное x нам нужно 12:6=2
Ответ: по 2 яблока у каждого ребенка.

Рассмотрим подробно пример 12:6=2

Число 12 называется делимым. Это число, которое делят.
Число 6 называется делителем. Это число, на которое делят.
И результат деления число 2 называют частным. Частное показывает во сколько раз делимое больше делителя.

В буквенном виде деление выглядит так:
a:b=c
a – делимое,
b – делитель,
c – частное.

Так что же такое деление?

Деление – это действие, обратное умножению. По произведению одного множителя мы можем найти другой множитель.

Деление проверяется умножением, то есть:
a:b=c, проверка с⋅b=a
18:9=2, проверка 2⋅9=18

Неизвестный множитель.

Рассмотрим задачу:
В каждой упаковке по 3 штуки елочных шаров. Чтобы нарядить елку нам нужно 30 шаров. Сколько нам нужно взять упаковок с елочными шарами?

Решение:
x – неизвестное количество упаковок шаров.
3 – штуки в одной упаковки шаров.
30 – всего шаров.

x⋅3=30 нам нужно столько раз взять по 3, чтобы получилось в итоге 30. x – это неизвестный множитель. То есть, чтобы найти неизвестный множитель нужно, произведение поделить на известный множитель.
х=30:3
х=10

Ответ: 10 упаковок шаров.

Неизвестное делимое.

Рассмотрим задачу:
В каждой упаковке по 6 цветных карандашей. Всего упаковок 3 штуки. Сколько всего карандашей было, до того пока их не разложили по упаковкам?

Решение:
x – всего карандашей,
6 – карандашей в каждой упаковке,
3 – упаковки карандашей.

Запишем уравнение задачи в виде деления.
x:6=3
x – это неизвестное делимое. Чтобы найти неизвестное делимое надо, частное умножить на делитель.
х=3⋅6
х=18

Ответ: 18 карандашей.

Неизвестный делитель.

Разберём задачу:
Было 15 шаров в магазине. За день в магазин пришло 5 покупателей. Покупатели купили равное количество шаров. Сколько шаров купил каждый покупатель?

Решение:
х – количество шаров, которое купил один покупатель,
5 – количество покупателей,
15 – количество шаров.
Запишем уравнение задачи в виде деления:
15:х=5
х – в данном уравнении является неизвестным делителем. Чтобы найти неизвестный делитель, мы делимое делим на частное.
х=15:5
х=3

Ответ: по 3 шара у каждого покупателя.

Свойства деления натурального числа на единицу.

Правило деления:
Любое число, деленное на 1 результатом будет тоже самое число.

7:1=7
a:1=a

Свойства деления натурального числа на нуль.

Рассмотрим пример: 6:2=3, проверить правильно ли мы поделили можно умножением 2⋅3=6.
Если мы 3:0, то сделать проверку мы не сможем, потому что любое число умноженное на нуль будет нуль. Поэтому запись 3:0 не имеет смысла.
Правило деления:
Делить на нуль нельзя.

Свойства деления нуля на натуральное число.

0:3=0 эта запись имеет смысл. Если мы ничего поделим на три части то получим ничего.
0:a=0
Правило деления:
При делении 0 на любое натуральное число не равное нулю, результат всегда будет равен 0.

Свойство деления одинаковых чисел.

3:3=1
a:a=1
Правило деления:
При делении любого числа на себя, не равное нулю, результат будет равен 1.

Вопросы по теме “Деление”:

В записи a:b=c назовите, что здесь является частным?
Ответ: a:b и c.

Что такое частное?
Ответ: частное показывает во сколько раз делимое больше делителя.

При каком значении m запись 0⋅m=5?
Ответ: при умножении на нуль в ответе всегда будет 0. Запись не имеет смысла.

Существует ли такое n, что 0⋅n=0?
Ответ: да, запись имеет смысл. При умножении любого числа на 0 будет 0, поэтому n – любое число.

Пример №1:
Найдите значение выражение: а) 0:41 б) 41:41 в) 41:1
Ответ: а) 0:41=0 б) 41:41=1 в) 41:1=41

Пример №2:
При каких значениях переменных верно равенство: а) х:6=8 б) 54:х=9

а) х – в данном примере является делимым. Чтобы найти делимое нужно частное умножить на делитель.
х – неизвестное делимое,
6 – делитель,
8 – частное.
х=8⋅6
х=48

б) 54 – делимое,
х – делитель,
9 – частное.
Чтобы найти неизвестный делитель, нужно делимое поделить на частное.
х=54:9
х=6

Задача №1:
У Саши 15 марок, а Миши 45 марок. Во сколько раз у Миши марок больше чем у Саши?
Решение:
Можно задачу решить двумя способами. Первый способ:
15+15+15=45
Нужно 3 числа 15, чтобы получить 45, следовательно, в 3 раза у Миши марок больше, чем у Саши.
Второй способ:
45:15=3

Ответ: в 3 раза у Миши марок больше, чем у Саши.

7 Числовые выражения. Буквенные выражения

Числовые выражения

Числовое выражение – это запись , состоящая из чисел и знаков действий между ними.

Например, 44 + 32

Значение выражения - это результат выполненных действий.

Например, в записи 44 + 32 = 76, значение выражения - это 76.

Буквенные выражения

Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.

В этих выражениях буквы могут обозначать различные числа. Число, которым заменяют букву, называют значением.

Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.

Чаще всего используются буквы:

a, b, c, d, x, y, k, m, n

8 Уравнение.Текстовые задачи

-

9 Решение типичных задач с помощью уравнений

Решение задачи обычно сводится к тому, чтобы путем логических рассуждений и вычислений найти значение какой-нибудь величины. Например, найти скорость, время, расстояние, массу какого-нибудь предмета или количество чего-то.

Такую задачу можно решить с помощью уравнения. Для этого искомое значение обозначают через переменную, затем путем логических рассуждений составляют и решают уравнение. Решив уравнение, производят проверку на то, удовлетворяет ли решение уравнения условиям задачи.

10 Действия с натуральными числами

К арифметическим или рациональным действиям над числами относят
сложение +,
вычитание -,
умножение x,
деление : (или /).

Только два из этих действий — сложение и умножение — определены на множестве натуральных чисел.

Действительно, деление и вычитание не всегда возможны на множестве.
Например:

5-10=-5

5:10=0.5

11 Делители и кратные натурального числа. Четные и нечетные натуральные числа. Число 0

Делителем натурального числа n называют число, на которое n делится без остатка.

Например:

делителем числа 9 является число 3

9 : 3 = 3 

делителем числа 9 не является число 4

9 : 4 = 2

Если число b делитель числа a , то a называют кратным числу b.

a : b = n

Например:

 12 : 6 = 2

двенадцать кратно шести или
двенадцать — кратное числа шесть.

Наименьшим кратным натурального числа является само это число.

Например: семь кратно семи, девять кратно девяти.

Четные и нечетные натуральные числа

 Натуральные числа бывают четными и нечетными. Четные числа - это те числа, которые оканчиваются цифрами 0; 2; 4; 6; 8. Нечетные числа - это те числа, которые оканчиваются цифрами 1; 3; 5; 7; 9.

Число ноль

Целое число, которое при сложении с любым числом или вычитании из него не меняет последнее, то есть дает результат, равный этому последнему; умножение любого числа на ноль дает ноль.

12 Признаки делимости натуральных чисел на 2, на 5, на 10, на 9 и на 3

Признак делимости на 2

Если последняя цифра в записи натурального числа четная (2, 4, 6, 8) или 0 , то это число делится на 2 без остатка.  

Числа   2, 4, 6, 8, 10 … , 220, 222, 224, 226, 228, … , 1200, 1202, 1204, 1206, 1208, 1210, 1212, 1214 … и т. д. делятся на 2 без остатка.

Например:

20 : 2 = 10

224 : 2 = 112

2336 : 2 = 1168

Если последняя цифра натурального числа нечетная (1, 3, 5, 7, 9), то число на 2 без остатка не делится. 

Признак делимости на 5

Натуральное число делится на 5 без остатка в том случае, если оно оканчивается на 0 или на 5.   

Числа 5, 10, 15, 20 … , 220, 225, … и т. д. делятся на 5 без остатка. 

Например:

20 : 5 = 4;

225 : 5 = 45;

2335 : 5 = 467

Признак делимости на 10

Натуральное число делится на 10 без остатка только в том случае, если оно оканчивается на нуль. Если последняя цифра натурального числа не 0, то число на 10 без остатка не делится.  

Числа 10, 20, 30 … , 220, 1200, 1210 … и т. д. делятся на 10 без остатка. 

Например: 

 20 : 10 = 2
 220 : 10 = 22
 2330 : 10 = 233

Признак делимости на 3

Натуральное число делится на 3 без остатка, если сумма его цифр кратна трем. 

Число 762 делится на 3 без остатка, так как сумма его цифр: 

7 + 6 + 2 = 15 — кратна 3  ( 15 : 3=5 ).   

Число 4587 делится на 3 без остатка, так как сумма его цифр:           

4 + 5 + 8 + 7 = 24 — кратна 3  ( 24 : 3=8 ).   

Признак делимости на 9

Признак делимости на 9 такой же, как и на 3. Натуральное число делится на 9 без остатка, если сумма его цифр кратна девяти.

Число 765 делится на 9 без остатка, так как сумма его цифр: 

7 + 6 + 5 = 18 — кратна 9  ( 18 : 9=2 ).   

Число 4698 кратно 9, так как сумма его цифр: 

4 + 6 + 9 + 8 = 27 — делится на 9 без остатка         ( 27 : 9=3 ). 

13 Простые и составные числа. Разложение чисел на простые множители

Всякое составное число можно разложить на простые множители. При любом способе получается одно и то же разложение, если не учитывать порядка записи множителей.   

Последовательность действий при разложении на простые множители: 

1. Проверяем, не является ли предложенное число простым. 
2. Если нет, то подбираем, руководствуясь признаками деления делитель, из простых чисел начиная с наименьшего   (2, 3, 5 …). 
3. Повторяем это действие до тех пор, пока частное не окажется простым числом. 

Разложим на простые множители число 27: 

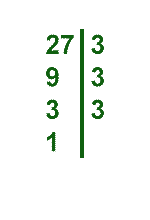
27 не является простым. 
27 на 2 не делится. 
27 делится на 3, получаем   27 : 3 = 9 . 
9 на 2 не делится. 
9 делится на 3,       9 : 3 = 3. 
3 простое число. 
Результат:   27 = 3 • 3 • 3. 

14 Общий делитель нескольких чисел. Наибольший общий делитель

Наибольший общий делитель (НОД) двух и более чисел — это самое большее натуральное число, на которое эти числа делятся без остатка.

Например:  у чисел 12 и 8 наибольший общий делитель (НОД) равен 4, 
а у чисел 20 и 35   (НОД) равен 5 

Для нахождения наибольшего общего делителя двух или более чисел, например 36 и 24 , надо: 

1) Разложить их на простые множители; 

36 = 2 • 2 • 3 • 3

24 = 2 • 2 • 2 • 3

2) В группах множителей ( 2 • 2 • 3 • 3 )  и  ( 2 • 2 • 2 • 3 ) , входящих в разложение этих чисел, оставляем только совпадающие множители.

( 2 • 2 • 3 )              и              ( 2 • 2 • 3 )    

3) Найти произведение оставшихся множителей. 2 • 2 • 3 = 12  

Наибольший общий делитель чисел   36 и 24   равен   12.

Если все данные числа делятся на одно из них, то это число и является наибольшим общим делителем данных чисел.

Например: у чисел   12 , 36 и 48   НОД   =   12 .   

15 Общее кратное нескольких чисел. Наименьшее общее кратное

Наименьшим общим кратным (НОК) натуральных чисел a и b называют наименьшее натуральное число, которое кратно и a , и   b.

Чтобы найти наименьшее общее кратное нескольких натуральных чисел, например 6 и 8 ,   надо: 

1) разложить их на простые множители; 

2) выписать множители, входящие в разложение одного из чисел;

3) домножить их на недостающие множители из разложений остальных чисел; 

4) найти произведение получившихся множителей. 

Найдем наименьшее общее кратное чисел 24   и   36: 

1) разложим их на простые множители; 

24   =   2   •   2   •   2   •   3

36   =   2   •   2   •   3    •   3 

2 , 2 и 3 есть в разложении числа 24     ( вычеркиваем их );

2) выпишем множители, входящие в разложение числа 24 ; 

2 • 2 • 2 • 3

3) домножим их на недостающий множитель из разложения числа 36 ; 

2 • 2 • 2 • 3             •             3 

4) найти произведение получившихся множителей. 

2 • 2 • 2 • 3 • 3   =   72; 

НОК ( 24 и 36 ) = 72 .

16 Формулы

Свойства сложения и вычитания

1. а+b=b+a

2. (a+b)+c=a+b+c=a+c+b=a+(b+c)

3. a-b+c=a+c-b (переставляем вместе со знаками)

4. a+b-c=a-c+b (переставляем вместе со знаками)

5. a-(b+c)= a-b-c (минус перед скобкой меняет знаки на противоположные)

6. a-(b-c)= a-b+c (минус перед скобкой меняет знаки на противоположные)

7. a-b-c=a-(b+c)

8. а-0=а

9. а+0=а

10. а-а=0

11. (a+b)c=ac+bc

12. (a-b)c=ac-bc

Формула пути

S=v·t

v=S:t

t=S:v

где S – расстояние, v – скорость, t – время

Формула радиуса

r = 2d, где r – радиус, d – диаметр

17 Правильные и неправильные дроби

Дробь в математике — число, состоящее из одной или нескольких равных частей (долей) единицы. Дроби являются частью поля рациональных чисел. По способу записи дроби делятся на два формата: обыкновенные вида. и десятичные вида.

Дроби, у которых числитель больше либо равен знаменателю называются неправильные, а те у которых числитель меньше знаменателя правильными.     

18 Основное свойство дроби

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь. Это свойство называют основным свойством дроби.   

19 Сокращение дробей

Сократить дробь – это значит разделить ее числитель и знаменатель на их положительный и отличный от единицы общий делитель

20 Наименьший общий знаменатель. Приведение дробей к общему знаменателю. Сравнение обыкновенных дробей

Так для чего нужен общий знаменатель, или когда нужен общий знаменатель? Ответ довольно прост, мы имеем право дроби складывать и вычитать только когда у данных дробей есть общий знаменатель. Поэтому важно понять, как находить общий знаменатель.

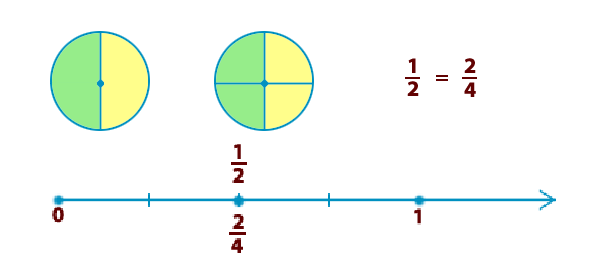
На рисунке вы видите круг, разделенный на четыре части.

Две части вместе, например желтые, составляют половину круга. 

Делаем вывод, что    1/2 = 2/4

На координатном луче эти дроби также расположены в одной и той же точке. 

Равные дроби обозначают одно и то же дробное число

21 Сложение и вычитание дробей с разными знаменателями

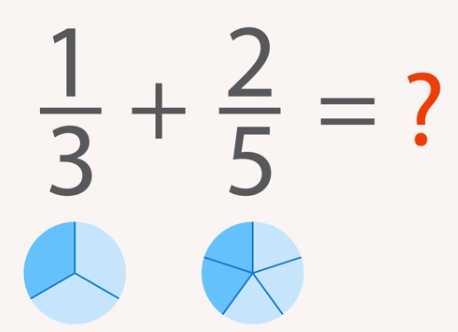
Если мы заменим одну из дробей на эквивалентную (равную ей), то сумма, очевидно, не изменится.

Для дроби 1/3 существует бесконечное множество дробей, которые ей эквивалентны. Чтобы их получить, нужно одновременно умножать и числитель, и знаменатель на одно и то же число (2, 3, 4 и т.д.). Тем самым мы получим цепочку эквивалентных дробей:

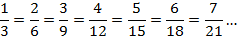
Аналогично поступим и со второй дробью:

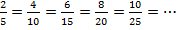
Мы можем заменить исходные дроби эквивалентными. Но выбирать нужно так, чтобы новые дроби имели одинаковые знаменатели, ведь мы уже умеем их складывать. Одинаковый знаменатель у дробей 5/15 и 6/15, заменим исходные дроби на них:

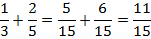
Если нам нужно сложить две дроби, то смотрим на их знаменатели.

1) Если знаменатели одинаковые, то складываем сразу.

2) Если знаменатели разные, то заменяем исходные дроби эквивалентными, чтобы новые дроби имели одинаковые знаменатели. И складываем эти новые дроби.

22 Сложение и вычитание смешанных чисел

Чтобы сложить смешанные числа, надо:

• привести дробные части к наименьшему общему знаменателю;
• сложить отдельно целые и дробные части;
• если необходимо, сократить дробную часть;
• если дробная часть суммы получится неправильной дробью, то выделить из неё целую часть и полученное число прибавить к целой части суммы.

Чтобы вычесть смешанные числа, надо:

• привести дробные части к наименьшему общему знаменателю;
• если дробная часть уменьшаемого меньше дробной части вычитаемого, «занять» единицу из целой части;
• вычесть отдельно целые и дробные части;
• если необходимо, сократить дробную часть.

23 Умножение обыкновенных дробей

Чтобы перемножить обыкновенные дроби, необходимо умножить числитель на числитель (получим числитель произведения) и знаменатель на знаменатель (получим знаменатель произведения).

24 Нахождение дроби от числа

Чтобы найти дробь от числа, нужно умножить число на эту дробь

25 Умножение смешанных чисел

Умножение смешанных чисел можно свести к умножению обыкновенных дробей. Для этого достаточно выполнить перевод смешанных чисел в неправильные дроби. При умножении дроби на натуральное число, мы должны ее числитель умножить на это число, а знаменатель оставить без изменения.

Правило умножения смешанных чисел:

• Во-первых, умножаемые смешанные числа нужно заменить неправильными дробями;
• Во-вторых, нужно воспользоваться правилом умножения дроби на дробь.

Рассмотрим примеры применения этого правила при умножении смешанного числа на смешанное число.

26 Взаимно обратные числа

Два числа, произведение которых равно единице, называются взаимно обратными.

27 Деление обыкновенных дробей. Деление смешанных чисел

Деления является обратным умножению. При делении неизвестный множитель  находится при известном произведении и другого множителя, где и сохраняется его данный смысл с обыкновенными дробями.

Деление смешанных чисел:

28 Нахождение числа по его дроби

Чтобы найти число по данному значению его дроби, надо это значение разделить на дробь.