Постановка задачи. Торговое предприятие (предприятие оптовой торговли), исходя из специализации, может реализовать 4 группы товаров Tj (). Пусть общая площадь торговых залов P (тыс. м2),  Pj (м2) – норматив складских площадей на содержание товаров j-ой группы; R (тыс. чел.-ч.) – фонд рабочего времени работников, rj (чел.-ч.) – плановый норматив затрат времени работников на единицу товарооборота j-ой товарной группы. Пусть B (тыс. д.е.) – допустимые издержки обращения, bj (д.е.) – плановый норматив издержек обращения на единицу товарооборота j-ой товарной группы. S (тыс. ед.) – общий объем товарных запасов. Sj (ед.) – норматив товарных запасов на единицу товарооборота j-ой товарной группы. Q (тыс. д.е.) – плановый показатель товарооборота. qj – параметр товарооборота (средняя цена реализации), по j-ой товарной группе. Gj (тыс. д.е.) – минимально допустимые значения плана товарооборота по j-ой товарной группе. Cj (д.е.) – торговая прибыль в расчете на единицу товарооборота j-й группы (табл.).

Требуется:

1. определить план хозяйственной деятельности торгового предприятия, обеспечивающий максимум торговой прибыли при заданных ограничениях на складские площади, трудовые ресурсы, издержки обращения, товарные запасы, величину товарооборота и др.;
2. cделать анализ полученного решения;
3. дать экономическую интерпретацию двойственным оценкам и дополнительным двойственным переменным;
4. выявить «узкие места» на торговом предприятии и дать рекомендации по их «расшивке».

Порядок выполнения работы (на примере варианта 0)

1. Составление математической модели задачи.

Введем переменные: xj (ед.) – величина товарооборота j-й товарной группы. Тогда математическая модель задачи примет вид:

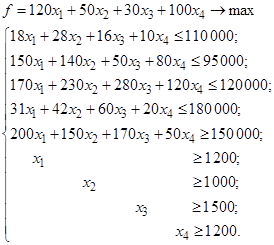
2. Ввод условий задачи.

Сделаем форму и введем исходные данные

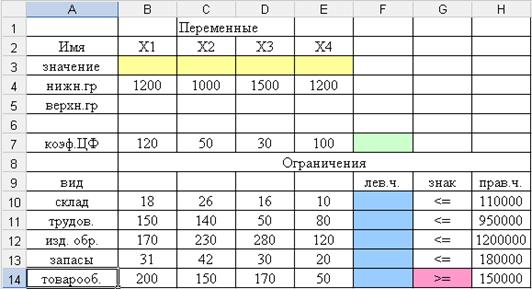
Ячейки В3:Е3 (под Х1 – Х4) являются искомыми для значений переменных, ячейка F7 предназначена для значения целевой функции, ячейки F10:F14 предназначены для внесения левой части ограничений задачи.

Чтобы получить значение целевой функции в ячейке F7,  воспользуемся функцией СУММПРОИЗВ. Для этого поместим курсор в ячейку F7, с помощью команды МАСТЕР ФУНКЦИЙ вызовем математическую функцию СУММПРОИЗВ. На экране появится диалоговое окно

В массив 1 вводим строку со значениями переменных, т.е. $B$3:$E$3 (знак $ ставим вручную для того, чтобы адрес не менялся при копировании формул). В массив 2 введем адрес строки коэффициентов целевой функции, т.е. В7:Е7. Заметим, что во все диалоговые окна адреса ячеек удобно вводить не с клавиатуры, а протаскивая мышь по ячейкам, чьи адреса следует ввести.

Далее копируем формулу из ячейки F7 в столбец «Левые части ограничений»

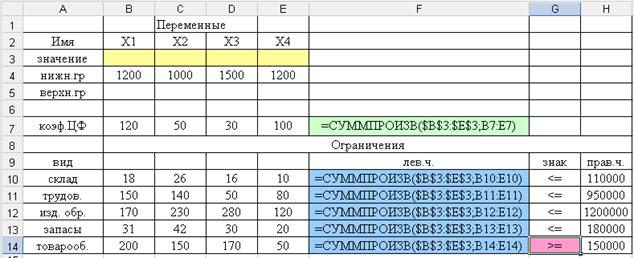
Решение задачи осуществляется в следующей последовательности.

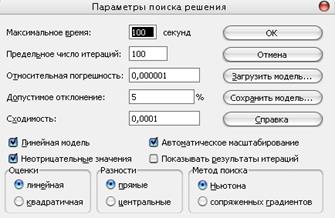
Командой Поиск решения из меню Сервис откроем диалоговое окно Поиск решения и занесем в него необходимые данные:

Установить целевую функцию – адрес ячейки, отведенной под значение целевой функции, т.е. F7;

Равной: – максимальному значению;

Изменяя ячейки – адреса изменяемых значений переменных, т.е. B3:E3;

Ограничения – Добавить…

На экране появится диалоговое окно Добавление ограничения

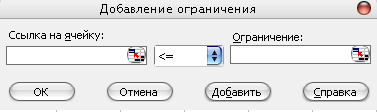
Здесь вводим граничные условия на переменные: В3:Е3 ³ В4:Е4 (выделяя соответствующие ячейки мышкой). Добавить: F10:F13 £ H10:H13, Добавить F14 ≥ H14, ОК.

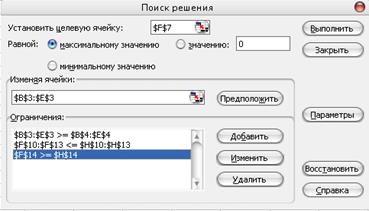
Далее командой Параметры вызываем диалоговое окно Параметры поиска решения и устанавливаем флажки: Линейная модель, Неотрицательные значения, Автоматическое масштабирование. ОК.

Возвращаемся в диалоговое окно Поиск решения и, щелкнув по кнопке Выполнить, находим оптимальное решение задачи. Если решение не найдено, окно выведет соответствующее сообщение. В противном случае на экране появляется диалоговое окно Результаты поиска решения. Для анализа полученного оптимального решения предусмотрены три типа отчетов. Помечаем для вывода два из них: по результатам, по устойчивости.

Нажимаем ОК. В результате получим оптимальное решение на рабочем листе и дополнительно два листа отчетов.

Оптимальное решение:

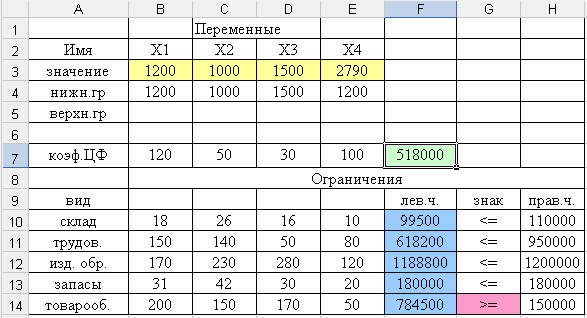
Отчёт по результатам:

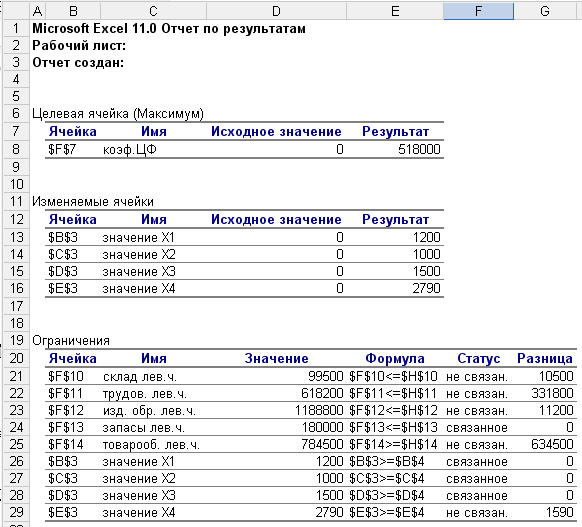
Отчет по результатам содержит данные о значении целевой функции (Результат – 518 000), значениях переменных (вторая таблица) и данные по всем ограничениям задачи (третья таблица). Для ограничений в столбце Формула приведены зависимости ограничений задачи. В столбце Значение приведены величины левых частей ограничений. В столбце Статус – связанное или не связанное обозначает: обращается ли соответствующее ограничение в строгое равенство или неравенство соответственно при подстановке в него найденных значений переменных оптимального плана (т.е. Х1* – Х4*); Разница – разница левой и правой частей ограничений.

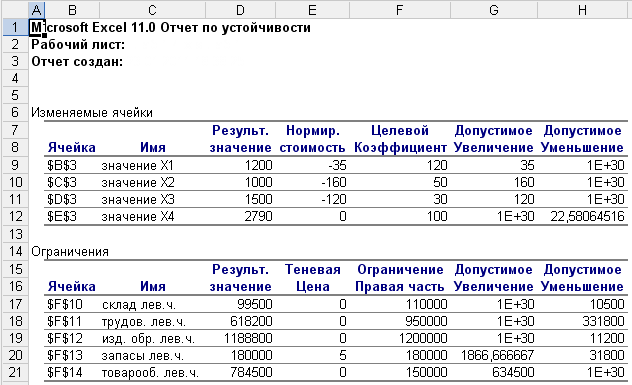
В отчете по устойчивости дан анализ по переменным и ограничениям. В первой таблице приведены следующие данные: результирующие значения основных переменных задачи; нормированная стоимость – значения дополнительных двойственных переменных; коэффициенты целевой функции и допустимые значения приращения коэффициентов целевой функции (границы устойчивости).

Во второй таблице: значения левых частей ограничений задачи; теневые цены – двойственные оценки (значения основных двойственных переменных); значения приращения правых частей ограничений задачи, при  которых сохраняется структура оптимального набора переменных, входящих в оптимальное решение задачи (границы устойчивости). См. приложение А.

3. Оформление отчета о проделанной работе.

План отчета:

1. Фамилия, Имя Отчество; группа, факультет, № варианта.
2. Экономико-математическая модель.
3. Полный экономический анализ результатов решения исходной задачи.
4. Экономическая интерпретация двойственных оценок и дополнительных двойственных переменных.
5. Выявление «узких мест» на торговом предприятии и предлагаемые рекомендации по их «расшивке».