Динамические модели в экономике

Определение устойчивости. Виды устойчивости.

Под устойчивостью, или стабильностью, системы в широком смысле понимается свойство системы возвращаться в некоторое установившееся состояние или режим после нарушения последнего какими-либо внешними или внутренними факторами.

Основным содержанием теории устойчивости является иссле­дование влияния возмущающих воздействий на поведение си­стемы. При этом под возмущающими факторами понимаются силы, обычно неизвестные заранее, которые как вследствие своей неопределенности, так и вследствие относительной мало­сти по сравнению с основными силами, не учитываются при описании движения системы.

Система может иметь и несколько состояний устойчивого и неустойчивого равновесия.

Относительно некоторого возмущения, действующего на си­стему, ее состояние равновесия (или цикл) может характери­зоваться несколькими типами устойчивости. Если система возвращается в состояние равновесия или цикличности при любых возможных воздействиях на нее (при любых возмуще­ниях), то равновесие называют абсолютно устойчивым. Если система при возмущениях возвратится в состояние равновесия только из некоторой обла­сти, то равновесие называют устойчивым относительно этой об­ласти. Наконец, если после воздействия на систему она сохраняет новое состояние, вызванное этим воздействием, то систему называют безразлично устойчивой. Во всех остальных случаях, кроме перечисленных выше, си­стема является неустойчивой.

Существует также понятие асимптотической устойчивости, под которой пони­мается устойчивость с неограниченным приближением во времени возмущенного движения к невозмущенному.

Устойчивость поведения систем, как правило, является по­ложительным свойством, обеспечивающим их нормальное целе­направленное функционирование и сохранение целостности в экстремальных условиях. Однако в ряде случаен устойчивость отражает инерционность, косность систем, ограничивающую возможность управления ими.

Устойчивость представляет собой одно из проявлений эмерджентности систем. Устойчивость является свойством всей системы в целом, а не какой-либо ее отдельной части. Система состоящая из нескольких устойчивых подсистем, может оказаться неустойчивой, и наоборот, при объединении некоторого количества неустойчивых подсистем может возникнуть устойчивая система (в зависимости от способа такого объединения).

Устойчивость по Ляпунову (1 вариант)

Понятие устойчивости по Ляпунову характеризует траекторию с точки зрения поведения соседних траекторий, располагающихся в ее окрестности. Предположим, что система при старте из начальной точки X порождает траекторию X(t). Рассмотрим другую траекторию той же системы Y(t), стартовая точка которой близка к X. Если обе траектории остаются близкими в любой последующий момент времени, то траектория X(t) называется устойчивой по Ляпунову.

Наглядная иллюстрация устойчивости по Лагранжу, Пуассону и Ляпунову приводится на рис. Когда говорят просто об устойчивой траектории, то всегда имеется в виду устойчивость по Ляпунову.

 

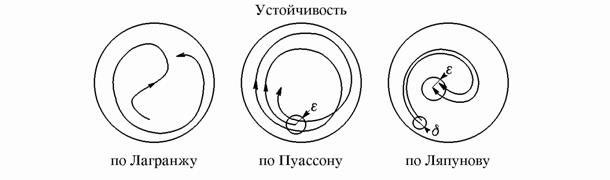
Определение устойчивости по М. Я. Ляпунову

Невозмущенное движение (при Δxi∞=0) называется устойчивым по отношению к переменным xi, если при всяком заданном положительном числе A2, как бы мало оно ни было, можно выбрать другое положительное число λ2(A2) так, что для всех возмущений Δxi0, удовлетворяющих условию:

i=0n∑(μi2(Δxi0)2)≤λ2,

возмущенное движение будет для времени t≥T удовлетворять неравенству:

i=0n∑(μi2(Δxi)2)≤A2,

где: μi – коэффициенты, уравновешивающие размерности величин Δxi0.

Если с течением времени limΔxi→0, то система асимптотически устойчива.

Особенности определения устойчивости по Ляпунову.
1. Возмущения накладываются только на начальные условия, что физически говорит о том, что возмущенное движение происходит при тех же источниках энергии, что и невозмущенное.
2. Устойчивость рассматривается на бесконечно большом интервале времени.
3. Возмущения предполагаются малыми.
Тем не менее, методы развитые Ляпуновым лежат в основе исследования других видов устойчивости движения.

Если сколь угодно малые изменения начальных данных могут сильно изменять решение, то это соответствует неустойчи­вому состоянию системы. Задача определения устойчивости объекта, сводится к нахождению условий, при которых достаточно малое изменение на­чальных данных приводит к сколь угодно малому изменению решения.

По определению, предложенному Ляпуновым, решение y*i(t) (i = 1, 2,…, п) устойчиво, если в любой задан­ной области ε допустимых отклонений от состояния равнове­сия можно подобрать такую область начальных условий d, включающую состояние равновесия, что траектория любого движения, начавшегося внутри d, никогда не достигнет границ области ε.

Существует также понятие асимптотической устойчивости, под которой пони­мается устойчивость с неограниченным приближением во времени  возмущенного движения к невозмущенному. Таким образом, если устойчивое решение y*i(t) (i = 1, 2,…, п) при t ® ∞ удовлетворяет условию 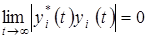для всякого решения yi(t), то имеет место асимптотическая устойчивость.

Понятие динамической системы. Структура динамических систем.

Элементы теории динамических систем

 • Основные понятия теории динамических систем

• Регулярная и хаотическая динамика

 • Характеристики динамического хаоса

Динамическая система – любой объект или процесс, для которого однозначно определено понятие состояния, как совокупности некоторых величин в некоторый момент времени, и задан закон, описывающий эволюцию начального состояния с течением времени.

Важнейшим свойством динамических систем является их устойчивость, т.е. сохранение системой своей базовой структуры и основных выполняемых функций в течение определенного времени и при относительно небольших и разнообразных внешних воздействиях и внутренних возмущениях.

Различают абстрактные динамические системы с дискретным временем и системы с непрерывным временем.

В системах с дискретным временем, которые традиционно называются каскадами, поведение системы (или, что то же самое, траектория системы в фазовом пространстве) описывается последовательностью состояний. В системах с непрерывным временем, которые традиционно называются потоками, состояние системы определено для каждого момента времени на вещественной или комплексной оси. Каскады и потоки являются основным предметом рассмотрения в символической и топологической динамике.

Все динамические системы можно разделить на два типа. В системах первого типа (более простых) между вектором входных величин Х и вектором выходных величии Y существует однозначная функциональная связь. Следовательно, задание вектора входных величин полностью определяет вектор выход­ных величин.

В системах втоpoгo типа (более сложных), к которым можно отнести большинство современных технических кибернетиче­ских систем и практически все биологические и экономические системы, имеют место дне ступени функциональных связей. Одна из них описывает зависимость внутреннего состояния си­стемы Z от вектора входных величии Х, другая –зависимость вектора выходных величин У от множества внутренних пара­метров системы (вектора состояния Z) и вектора входных ве­личин X. Таким образом, при исследовании систем второго типа, представляющих для нас наибольший интерес, вместо простой зависимости между входом и выходом Y(t) = f [X(t)] рассматривается более сложная зависимость

Y(t) = f [X(t), Z(t)].                  

Подавляющее большинство динамических систем представ­ляют объекты, которые описываются системой обыкновенных дифференциальных уравнений.

Системы обыкновенных дифференциальных уравнений мо­гут успешно применяться и для описания ряда процессов в эко­номике, в частности, при изучении глобальных проблем дина­мики развития народного хозяйства для построения так называемых макроэкономических моделей экономики страны, рассматриваемой как одно целое.

Основное содержание теории динамических систем — это исследование кривых, определяемых дифференциальными уравнениями. Сюда входит разбиение фазового пространства на траектории и исследование предельного поведения этих траекторий: поиск и классификация положений равновесия, выделение притягивающих (аттракторы) и отталкивающих (репеллеры) множеств (многообразий). Важнейшие понятия теории динамических систем — устойчивость (способность системы сколь угодно долго оставаться около положения равновесия или на заданном многообразии) и грубость (сохранение свойств при малых изменениях структуры динамической системы; “грубая система — это такая, качественный характер движений которой не меняется при достаточно малом изменении параметров”)

Модели Мальтуса и Ферхюльста

Модель Мальтуса описывает размножение популяции со скоростью, пропорциональной ее численности.

Рождаемость характеризует частоту появления новых особей в популяции. Различают рождаемость абсолютную и удельную. Абсолютная рождаемость - число особей, появившихся в популяции за единицу времени. Удельная рождаемость выражается в числе особей на особь в единицу времени

Введем обозначения:

N(t) – численность населения в момент времени t.

r – скорость прибыли

s –скорость убыли

∆t – промежуток времени

За некоторый малый промежуток времени ∆t в популяции произойдут изменения: часть индивидуумов погибнет или эмигрирует, но появятся новорожденные, а также иммигранты.  Математически это запишется так:

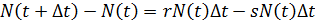
Разделим обе части на ∆t

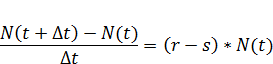
Переход к пределу при ∆t→0  приводит к дифференциальному уравнению:

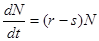
Решением уравнения с начальным условием 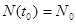 будет функция

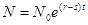
Основные предположения этой задачи:

Коэффициенты r и s являются постоянными и не зависят от времени. Это подразумевает, что популяция не ограничивается ни питанием, ни площадью, ни  другими популяциями. Кроме того, не учитывается внутренняя структура популяции.

В общем случае скорость прибыли и убыли зависят от N  и  t. В популяциях, являющихся компонентами стабильных экосистем обычно всегда обнаруживается статистически достоверная корреляция между этими величинами. Единственная популяция,  для которой данная корреляция положительна – это популяция человека.

Экспоненциальная форма динамики роста численности колонии микроорганизмов в соответствии с системой уравнений уровнений выглядит так:

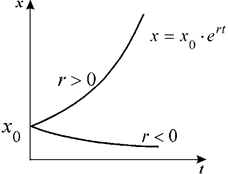
На основании этих выводов Мальтус говорит о необходимости ввести ограничения на рождаемость, в особенности для беднейших слоев общества.

Модель Ферхюльста

Впервые системный фактор, ограничивающий рост популяции, описал Ферхюльст в уравнении логистического роста.

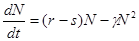
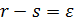 – коэффициент естественного прироста

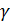 –  коэффициент «самоотравления»

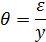
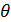 – коэффициент  «насыщения»

Это уравнение обладает двумя важными свойствами. При малых х численность возрастает экспоненциально,  при больших – приближается к определенному пределу 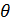. Эта величина, называемая емкостью популяции,  определяется ограниченностью пищевых ресурсов, мест для гнездования, многими другими факторами, которые могут быть различными для различных видов.

Уравнение Ферхюльста можно решить аналитически. Ход решения следующий. Произведем разделение переменных:

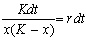
Представим левую часть в виде суммы и проинтегрируем

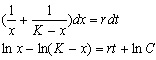
Переходя от логарифмов к переменным, получим:

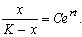
Здесь С - произвольная постоянная, которая определяется начальным значением численности x0:

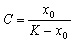
Подставим это значение С в формулу

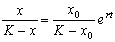
Отсюда получим решение - зависимость численности от времени:

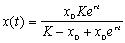
График функции  при разных начальных значениях численности популяции.

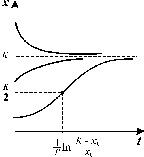
Eсли начальное значение х0 < К/2, кривая роста имеет точку перегиба. Если х0 > К, численность со временем убывает.

Возможны и другие механизмы возникновения колебаний численности (учет возрастной структуры популяции, наличие случайных возмущений и т.д.) процессы.

Уравнение Ферхюльста графически отображается в виде S- образной кривой. Эта кривая называется логистической кривой, а рост численности, соответствующий уравнению -логистическим. Исследуя кривую, можно сказать, что максимальная скорость роста достигается, когда численность равна K/2. В некоторый момент численность стабилизируется и остается постоянной величиной.

Популяции, существующие в условиях ограниченных ресурсов, часто хорошо подчиняются правилам логистического роста. Например, когда овцы были завезены в Тасманию, рост их стада описывался логистической кривой. Но правила логистического роста применимы не ко всем случаям. Например, у размножающихся половым путем видов, при слишком малой численности мала вероятность встреч особей разного пола и размножение может вообще прекратиться.

Для реализации модели в среде электронных таблиц уравнение (3) следует представить в дискретном виде

N(i+1)=N(i)*r*(1-N(i)/K)

где N(i) - численность популяции в i-й момент времени;

r -удельная скорость роста популяции (рождаемость/ смерность);

К- емкость среды.

Точным решением уравнения (4) является логистическая функция, S-образная кривая.

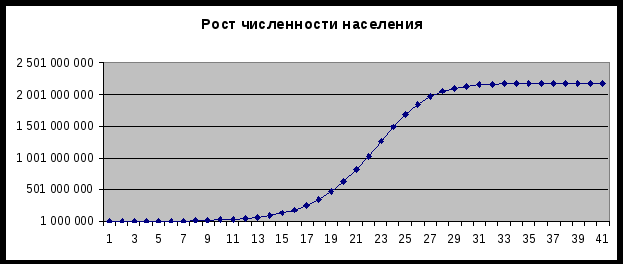
Существуют две стратегии роста численности популяции:

• первая предполагает бурное размножение и короткую продолжительность жизни особей;
• а вторая стратегия — низкий темп размножения и долгую жизнь.

Диффузионная модель Басса

Данная модель описывает диффузию новых продуктов, суть которой состоит в следующем:

Пусть существует некоторый  рынок, на  котором  появляется принципиально  новый продукт (товар  или  услуга), не  имеющий  аналогов  и, соответственно, конкуренции со стороны других продуктов. Этот продукт создает новый спрос, т.е. появляется  определенное  количество  людей, желающих приобрести  этот  продукт  или  уже  совершивших  его  покупку. Тогда доля  покупателей, совершающих  акт  покупки  в  момент  времени ( t ), описывается формулой:

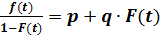, где

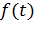  – доля  покупателей, совершающих  акт  покупки  в  момент времени ( t );  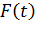  – доля покупателей, купивших продукт до момента времени ( t );  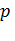 – коэффициент  инновации или  коэффициент  внешнего  влияния; 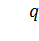– коэффициент имитации или коэффициент внутреннего влияния.

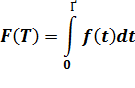
Модель предполагает, что рост количества потребителей инновационного продукта объясняется двумя эффектами:

• Эффект рекламы (эта категория покупателей  называется  новаторами) - принимается  постоянным  и выражается  коэффициентом  внешнего  влияния;
• Эффект межличностной коммуникации (эта  категория  покупателей называется  имитаторами) - увеличивается  по  мере роста  количества  людей, уже  совершивших  покупку (это  влияние предполагается  пропорциональным (коэффициент  внутреннего влияния) этому количеству).

На начальном этапе жизненного цикла продукта преобладает эффект рекламы, так как почти никто не знает о продукте и, соответственно, не может его купить. По мере роста количества потребителей эффективность рекламы снижается, но зато возрастает эффект межличностного общения.

Пусть m – число потенциальных покупателей продукта (потенциальный спрос), тогда  mf(t) = n(t)  -  число  покупок  в  момент  времени ( t ). Аналогично, mF(t) = N(t)  число  человек, уже  совершивших  покупку.