Метод анализа иерархий

Иерархическое представление проблемы, шкала отношений и матрицы парных сравнений; собственные векторы и собственные значения матриц. Оценка однородности суждений; синтез приоритетов на иерархии и оценка ее однородности. Учет мнений нескольких экспертов. Методы сравнения объектов относительно стандартов и копированием. Многокритериальный выбор на иерархиях с различным числом и составом альтернатив под критериями. Выбор и прогнозирование наилучшего обеспечения банковского кредита. Функционально-стоимостный анализ промышленной продукции. Рациональное распределение ресурсов между альтернативами. Аналитическое планирование на основе метода анализа иерархий. Решение задачи выбора интернет-провайдера методом анализа иерархий.

Метод Анализа Иерархий (МАИ) — математический инструмент системного подхода к сложным проблемам принятия решений. МАИ не предписывает лицу, принимающему решение (ЛПР), какого-либо «правильного» решения, а позволяет ему в интерактивном режиме найти такой вариант (альтернативу), который наилучшим образом согласуется с его пониманием сути проблемы и требованиями к её решению. Этот метод разработан американским математиком Томасом Саати, который написал о нем книги, разработал программные продукты и в течение 20 лет проводит симпозиумы ISAHP (англ. International Symposium on Analytic Hierarchy Process). МАИ широко используется на практике и активно развивается учеными всего мира. В его основе наряду с математикой заложены и психологические аспекты. МАИ позволяет понятным и рациональным образом структурировать сложную проблему принятия решений в виде иерархии, сравнить и выполнить количественную оценку альтернативных вариантов решения. Метод Анализа Иерархий используется во всем мире для принятия решений в разнообразных ситуациях: от управления на межгосударственном уровне до решения отраслевых и частных проблем в бизнесе, промышленности, здравоохранении и образовании. Для компьютерной поддержки МАИ существуют программные продукты, разработанные различными компаниями. Анализ проблемы принятия решений в МАИ начинается с построения иерархической структуры, которая включает цель, критерии, альтернативы и другие рассматриваемые факторы, влияющие на выбор. Эта структура отражает понимание проблемы лицом, принимающим решение. Каждый элемент иерархии может представлять различные аспекты решаемой задачи, причем во внимание могут быть приняты как материальные, так и нематериальные факторы, измеряемые количественные параметры и качественные характеристики, объективные данные и субъективные экспертные оценки. Иными словами, анализ ситуации выбора решения в МАИ напоминает процедуры и методы аргументации, которые используются на интуитивном уровне. Следующим этапом анализа является определение приоритетов, представляющих относительную важность или предпочтительность элементов построенной иерархической структуры, с помощью процедуры парных сравнений. Безразмерные приоритеты позволяют обоснованно сравнивать разнородные факторы, что является отличительной особенностью МАИ. На заключительном этапе анализа выполняется синтез (линейная свертка) приоритетов на иерархии, в результате которой вычисляются приоритеты альтернативных решений относительно главной цели. Лучшей считается альтернатива с максимальным значением приоритета.

Шаги метода анализа иерархий:

1. Представление исходной проблемы в виде иерархической структуры.

Цель составляет высший уровень иерархии (уровень 1). На этом уровне может находиться лишь один объект. На следующих вниз уровнях находятся критерии. По системе этих критериев оцениваются сравниваемые объекты (называемые «альтернативами»). Альтернативы располагаются на самом нижнем уровне. В задаче могут присутствовать несколько уровней критериев, но обычно применяют иерархии 3- уровневые (цель – критерии – альтернативы) и 4-х уровневые (цель – комплексные критерии – критерии – альтернативы).

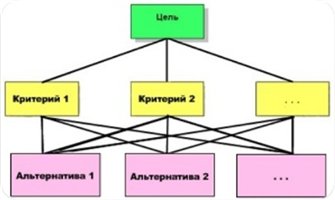
2. Вынесение экспертных суждений на каждом уровне иерархии по парным сравнениям: критерии сравниваются попарно по отношению к цели, альтернативы – попарно по отношению к каждому из критериев.

Соответственно заполняются матрицы парных сравнений: одна – для критериев, n матриц – для альтернатив; здесь n – количество критериев.

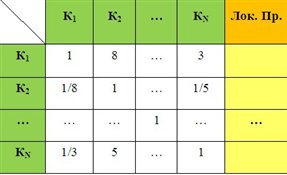
Операция парного сравнения: два объекта, находящихся на одном уровне сравниваются по своей относительной значимости для одного объекта высшего уровня. Если критерий имеет определенную числовую меру, например, масса, производительность, цена, то в качестве результата оценки удобно взять отношения соответствующих характеристик (заданных, или рассчитанных) в некоторой шкале отношений. Если критерий не имеет принятой меры, то сравнение в МАИ проводится с использованием специальной «шкалы относительной важности» (другие названия: «шкала 1-9», «шкала Саати»). Эта шкала имеет 9 степеней предпочтения, выбранные с учетом экспериментально установленных психофизиологических особенностей человека, выполняющего сравнение (таб. 3.1.2).

Шкала Саати

Степень предпо- чтения	Определение	Комментарии
1	Равная предпочтительность	Две альтернативы одинаково предпочтительны с точки зрения цели
2	Слабая степень предпочтения	Промежуточная градация между равным и средним предпочтением
3	Средняя степень предпочтения	Опыт эксперта позволяет считать одну из альтернатив немного предпочтительнее другой
4	Предпочтение выше среднего	Промежуточная градация между средним и умеренно сильным предпочтением
5	Умеренно сильное предпочтение	Опыт эксперта позволяет считать одну из альтернатив явно предпочтительнее другой
6	Сильное предпочтение	Промежуточная градация между умеренно сильным и очень сильным предпочтением
7	Очень сильное(очевидное) предпочтение	Опыт эксперта позволяет считать одну из альтернатив гораздо предпочтительнее другой: доминирование альтернативы подтверждено практикой
8	Очень, очень сильное предпочтение	Промежуточная градация между очень сильным и абсолютным предпочтением
9	Абсолютное предпочтение	Очевидность подавляющей предпочтительности одной альтернативы над другой имеет неоспоримое подтверждение

Числа из этой шкалы используются, чтобы показать, во сколько раз элемент с большей оценкой предпочтительности доминирует элемент с меньшей оценкой относительно общего для них критерия или свойства. В МАИ и МАС доминирование одного объекта над другим бывает а) по предпочтению; б) по важности; в) по вероятности.

При операции парного сравнения используют значения обратных оценок предпочтения: если преимущество i-той альтернативы по сравнению с j-той имеет одно из приведенных выше значений, то оценка предпочтения i-той альтернативы над j-той будет иметь обратное значение. То есть в МАИ все матрицы парных сравнений (МПС) являются обратно симметричными.

3. Математическая обработка матриц парных сравнений для нахождения локальных и глобальных приоритетов.

При точном процессе определения вектора локальных приоритетов задача сводится к нахождению собственного вектора матрицы парных сравнений:

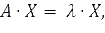
где A – матрица парных сравнений (МПС), X – n-мерный вектор, составленный из искомых приоритетов, λ - собственное значение МПС;

и последующего нормирования этого вектора:

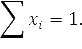
В рассматриваемой задаче искомым является вектор, соответствующий максимальному собственному значению.

Вектор локальных приоритетов может быть приближенно вычислен упрощенным способом:

Для каждой строки матрицы парных сравнений находим среднее геометрическое ее элементов:

Находим сумму всех этих средних геометрических.

Делим каждое среднее геометрическое на их сумму(«нормировка на единицу»). Результат - вектор локальных приоритетов данной матрицы.

В СППР NooTron определение вектора локальных приоритетов выполняется путем нахождения собственного вектора матрицы парных сравнений. Это трудоемкая задача (если «вручную»), но в состав практически всех математических пакетов включены средства для нахождения собственных значений и векторов матриц – Eigenvalues​​, Eigenvectors. При разработке МАИ для СППР была использована библиотека Efficient Java Matrix Library (EJML), что позволяет быстро и эффективно проводить матричные расчеты.

В МАИ есть возможность проверки согласованности экспертных оценок, т.е. чисел в каждой матрице парных сравнений. Для контроля согласованности этих оценок вводятся две связанные характеристики - индекс согласованности (CI) и отношение согласованности (CR):

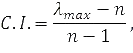
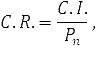
где Pn – это индекс согласованности для положительной обратно симметричной матрицы случайных оценок размера n*n; элементы этой матрицы получены случайным выбором из множества допустимых оценок, т.е. из чисел ряда {1/9, 1/8, 1/7, 1/6, 1/5, 1/4, 1/3, 1/2, 1, 2, 3, 4, 5, 6, 7, 8, 9}.

Таблица 3.1.3 – Значения индекса согласованности

N	1	2	3	4	5	6	7	8	9	10
Pn	0	0	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49

 

Допустимым считается отношение согласованности (CR), не превышающее 10 - 20%. Если CR выходит из этих пределов, то экспертам необходимо исследовать задачу и проверить свои оценки.

В результате обработки матриц получаем один вектор локальных приоритетов критериев размерности m (m - число критериев) и m векторов локальных приоритетов альтернатив размерности n (n - число альтернатив). Вектор локальных приоритетов критериев показывает их относительную значимость в задаче.

Вектор глобальных приоритетов альтернатив по отношению к цели вычисляется так: каждый компонент этого m-вектора – это скалярное произведение вектора локальных приоритетов критериев на m-вектор, составленный из локальных приоритетов альтернативы по данным критериям («профиль альтернативы»).

Профили дают в относительном виде достоинства и недостатки каждой из альтернатив и могут использоваться для определения путей улучшения альтернативы, например, для повышения конкурентоспособности.

Вектор глобальных приоритетов – это и есть решение задачи многокритериального ранжирования. На основании его можно, например, решить задачу выбора: альтернатива с максимальным значением глобального приоритета является лучшей по совокупности критериев с учётом относительной важности последних.