Математические методы анализа спроса и предложения

Методы определения потребностей. Эластичность спроса и потребления по цене и доходам. Статические, кинематические и динамические модели спроса. Функции  покупательского  спроса. Предельный  анализ  прогнозирование спроса. Структурные модели спроса. Особенности моделей спроса на  ИТ-продукцию. Модели оценки потребности в ИТ-ресурсах.

Функции покупательского спроса первичных, вторичных потребностей и на предметы роскоши

Л. Торнквист, предложил специальные виды функции спроса (функции Торнквиста) для трех групп товаров: первой необходимости, второй необходимости, предметов роскоши.

Функция Торнквиста для товаров первой необходимости имеет вид:

,

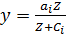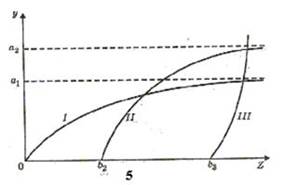
и отражает тот факт, что рост спроса на эти первоочередные товары с ростом дохода постепенно замедляется и имеет предел a1 (кривая спроса асимптотически приближается к прямой линии y=a1), график функции является вогнутой кривой I.

Функция спроса по Торнквисту на товары второй необходимости выражается формулой :

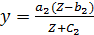 , где Z≥b2

Эта функция также имеет предел а2, но более высокого уровня; при этом спрос на эту группу товаров появляется лишь после того, как доход достигнет величины b2; график функции – вогнутая кривая II.

Наконец, функция Торнквиста для предметов роскоши имеет вид :

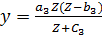 , где Z≥b3

Эта функция не имеет предела. Спрос на эти товары возникает только после того, как доход превысит величину b3, и далее быстро возрастает, так что график функции – выпуклая кривая III на

Кроме указанных функций, в аналитических моделях покупательского спроса используются также другие функции: степенные, S-образные и т.д.

Использование S-образных кривых в технологическом прогнозировании обусловлено простотой их применения, существующие методы определения параметров кривой позволяют в короткий срок сделать прогноз о развитии технологии. Но, несмотря на обширное использование моделей, можно выделить небольшие минусы. Они исходят из того, что с помощью модели прогнозирования трудно представить, как точно поведет себя в будущем развитие, а прогноз может быть и условным.

S-образная кривая необходима нам непосредственно для прогнозирования. Название этой функции дано по виду кривых, которые представляют ее графики. Функция  в общем случае может быть задана аналитически следующим выражением:

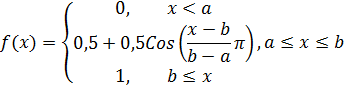
где a, b — некоторые числовые параметры, принимающие произвольные действительные значения с условием, что а < b. График этой функции изображен на рис. 1, при этом значения параметров соответственно равны a=3, b=6.

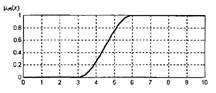
График S-образной функции для параметров а=3, b=6

Самые известные из таких кривых, это кривая Гомперца и логистическая кривая Перла-Рида.

Первая из них, кривая Гомперца, во многих работах исследователей стала эталоном для прогнозирования и получила свое название по фамилии известного математика Бенджамина Гомперца. Функция, задающая эту кривую, имеет вид:

yt=L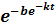

Вариант этой функции на графике:

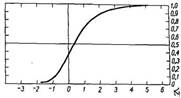
Кривая Гомперца

Кривая Гомперца, у которой L, b и k равны единице. Рассматривая кривую можно выделить четыре участка, границы между которыми более или менее условны. На первом участке прирост функции незначителен, на втором он постепенно увеличивается, на третьем прирост постоянен и на четвертом происходит замедление темпов, где функция приближается к значению K. В результате кривая напоминает латинскую букву S.

Теперь же перейдем к логистической кривой Перла-Рида. Если в модифицированной экспоненте уt = K +ebt вместо y ввести обратную величину, т.е. 1/yt, получим вторую S-образную кривую – логистическую кривую

1/yt = K + ebt ,

Логистическая кривая Перла-Рида:

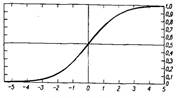
 Логистическую кривую в общем виде записывают:

,

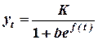где е – основание натуральных логарифмов; f(t) – некоторая функция от t ( обычно f(t) = - at),тогда, 

.

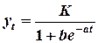Если b = 1, а вместо натуральных логарифмов перейти к десятичным логарифмам и принять условие, что f(t)=а + b(t), получим другой вид логистической кривой:

.
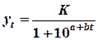